Hacker Dōjo Workshop：
Type: Quantum
Grant：300 USDT
Bounty：https://dorahacks.io/daobounty/105
Dojo hacker：Jan Ole Ernst
Bounty rewards：https://bscscan.com/tx/0x3e160f3aef9781cc161e0b3715ddb8ea1adb5822abf72d7c3133478525aeff79
Funded by Dōjo, please contact us before reprinting the article:
Telegram: @DoraDojo0
WeChat: @HackerDojo0
E-mail: hackerdojo0@gmail.com
A result from [1] is presented here which states the any local experiment which discriminates between a coherent superposition and an incoherent statistical mixture requires a minimum time proportional either to the mass or charge of the system. We proceed by explaining the difference between coherent superpositions and statistical mixtures, as well as explaining the desire for consistency with relativistic causality and then proceed to contextualise this result with respect to existing experiments testing microscopic and macroscopic quantum superpositions. Finally, the thought experiment which gives rise to the result will be presented for both massive and charged particles. This was a Dora Hacks Bounty Hunter submission in February 2023.
I. COHERENT SUPERPOSITIONS AND STATISTICAL MIXTURES
The difference between what is called a coherent superposition and a statistical mixture is subtle, and sometimes confusing, yet extremely important for understanding quantum mechanics and understanding the derivation presented in [1]. To illustrate this distinction, we consider the simplest possible example. Consider a two-dimensional Hilbert space spanned by two qubit states |L⟩, |R⟩, these two basis states (described in bra-ket notation) are orthogonal.
Without loss of generality, consider this states to be represented by two particular polarisation states of light, namely left and right circularly polarised. A simple example of a coherent superposition state reads:
Before making a measurement, i.e. while the state retains its coherence it does not have a uniquely deffned polarisation in the (L, R) basis. The polarisation of |ψ⟩ in this basis is determined upon making a measurement in the L, R basis and we project into one of the states |L⟩ or |R⟩. Thus upon making a measurement, the state decoheres, i.e. looses its coherence, and we observe one distinct polarisation. This is counter-intuitive, yet important and has been the subject of much debate amongst physicists (often described as the measurement problem). The absolute value squared of the
coefffcients of the two kets in Eq. 1 are the probabilities of measuring either |L⟩ or |R⟩. This state is pure, such that when we consider its density operator ρ = |ψ⟩⟨ψ|, it has 
is pure [2]. For a state to be pure it does not necessarily have to be in a coherent superposition, but importantly, mixed states are not pure since they do not satisfy the aforementioned condition.
Mixed states cannot be expressed as a single ket, yet we can express their density operator as follows:
Performing a measurement one σ in the (L, R) basis yields the same measurement statistics as performing a measurement on ρ = |ψ⟩⟨ψ|. This is somewhat paradoxical since the pure state and the mixed states differ fundamentally. The coherence between the two states expressed in Eq. 1 is not captured by this particular measurement. Switching our measurement basis however can resolve this paradox. If we measure in the (|+⟩, |−⟩) basis where 
then the coherent superposition |ψ⟩ and the mixed state σ give rise to completely different measurement outcomes.
The former always yields a result of |+⟩, whereas the latter would give rise to equi-probable measurement outcomes of |+⟩ and |−⟩. For a comprehensive introduction, confer Ref. [2].
II. RELATIVISTIC CAUSALITY
A desiderata for our physical theories is to satisfy Einstein’s theory of special relativity, formulated in 1905 [3].
Einstein expressed two particular physical principles which read:
- Relativity Principle The laws by which the states of physical systems undergo changes are independent of
whether these changes of states are referred to one or the other of two coordinate systems moving relatively to
each other in uniform translational motion. - Light Principle Any ray of light moves in the “stationary” system of co-ordinates with the determined velocity
c, whether the ray be emitted by a stationary or by a moving body.2
No experiments have been performed which violate these principles and in particular, the light principle constrains
the accessible regions of space-time. In particular, the causal past and causal future is limited to a space-time region
bounded by the the light-cone, since space-time regions which lie outside the lightcone would requires information
transfer at speeds greater than c, very much in tension with the light principle. This is visualised in Fig. 1. It was important to recap relativistic causality because it is the starting point of the derivation in [1] which is explained is Sec. IV.
Figure 1. Visual demonstration of the accessible regions of space-time taken from Re. [4].
III. MICROSCOPIC AND MACROSCOPIC SUPERPOSITIONS
Demostrations of microscopic superpositions are ubiqutous in experimental quantum physics. It was the entanglement
of spatially separated photons which lead to the Nobel prize in 2022 [5], beyond that coherent superpositions have been succesfully created and detected with electrons [6], neutrons [7], atoms [8], molecules [9] etc.
Investigations of macroscopic superpositions such as Schrödinger’s cat which is postulated to exist in a superposition of being dead and alive at the same time, go back to the historical origins of quantum mechanics. In general, nothing precludes standard quantum mechanics to be invalid at any particular length scale, yet practically and technically no such experiments have really been realised up to this day. Decoherence is a serious concern for such proposals, since large systems are hard to isolate from the environment and therefore any weak interaction with the environment destroys the initial coherence of the system irreversibly. The closest we have come is perhaps the recent experimental demonstration of a macroscopic superposition of a tartigrade with a superconducting qubit [10] or the entanglement of massive quantum optomechanical systems [11].3
IV. EXPERIMENTS TESTING MACROSOPIC SUPERPOSITIONS MUST BE SLOW
A. Thought Experiment
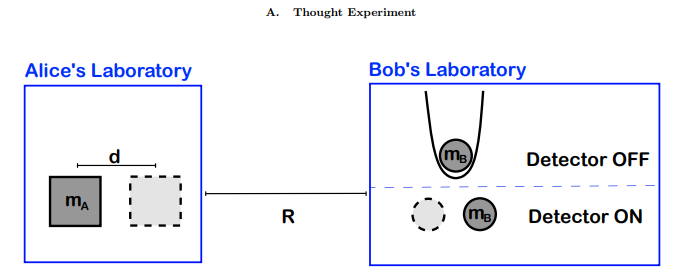
Figure 2. Visual demonstration thought experiment (taken from [1]). Alice prepares a microscopic mass mA in a quantum superposition of two spatial states separated by a distance d which are local to her. Bob who is a distance R >> d from Alice has a test mass prepared in the ground state of a narrow harmonic trap, he can send information to Alice by either; turning the detector off, or turning the detector on (removing the harmonic trap). There are two important time scales: TB the time required to generate entanglement between Alice and Bob’s particle if the detector is turned on and the time TA required for
Alice to make her local measurement that distinguishes between the statistical mixture and coherent superposition. Thus, information is transferred in a time TA + TB. This can equivalently be performed with charged particles.
Consider the thought experiment presented in Fig. 2. The protocol can be applied to quantum superpositions of large masses or large charges and will be described in what follows:
What the thought experiment insinuates is that Alice and Bob can communicate in such a way that Bob sends Alice4
one bit of information: whether his detector was on or off. A local measurement om Alice’s subsystem distinguishes
between the two insofar as detector off corresponds to a local coherent superposition and detector on corresponds to
a statistical mixture in Alice’s lab. For extremely large masses or charges it seems as though we can make TA + TB
arbitrarily small (confer Fig. 2. Does this mean that we can send messages at a speed faster than the speed of light -
violating relativistic causality [3]? .
As presented in Ref. [1] there are a variety of proposed solutions to this paradox. Perhaps it is actually impossible
to prepare such a macroscopic superposition or preserve coherence. Standard QM might not be able to adequately
explain this result either. This is not particularly insightful. Another option would be to say that once Alice
creates her local superposition, it is entangled with its own electric/gravitational ffeld and thus her state is always
mixed which makes the measurment outcome independent of Bob’s local operation. This precludes any sort of
communication, superluminal communication thus simply wouldn’t be possible. A third and ffnal option would be to
require a minimum time for Alice to locally discriminate between a coherent superposition and statistical mixture. If
entanglement generation TB happened in a
, where c is the speed of light, then we require:
The condition is recast as [1]:
The authors provide a series of proofs as to why the second solution is not a good one; the mass or charge mayaccelerate in the process of being placed into the coherent superposition (Eq. 3) such that acceleration leads to radiation and it becomes entangled with the emitted photons or gravitons respectively. Slow accelerations however
generate no photons or gravitons respectively (confer Appendix E in [1]). Similarly the particle cannot really be entangled with its static Couloumb ffeld since the expectation value of the electric ffeld depends on particle position, possibly being non-zero even if the modes of radiation are all in the vacuum and hence there cannot consistently be entanglement between the charge’s position and the Coloumb ffeld (confer Appendix F in [1]).
That leaves us only with the last proposal which requires a minimum time required for Alice to perform her measurement (see Eq. 3). It is perfectly consistent with the ffrst proposal in that it allows for decoherence to happen before this time in which case Alice can make no useful measurement anymore. Two particular cases of a charge and
mass are investigated and the measurements proposed are shown to be consistent with this limitation.
[1] A. Mari, G. D. Palma, and V. Giovannetti, Experiments testing macroscopic quantum superpositions must be slow,
Scientiffc Reports 6, 10.1038/srep22777 (2016).
[2] M. Nielsen and I. Chuang, Cambridge University Press (2000).
[3] A. Einstein, On the electrodynamics of moving bodies, Annalen Phys. 17, 891 (1905).
[4] T. Rogers, The proximity of light, (2016).
[5] G. Weihs, T. Jennewein, C. Simon, H. Weinfurter, and A. Zeilinger, Violation of bell’s inequality under strict einstein
locality conditions, Phys. Rev. Lett. 81, 5039 (1998).
[6] O. Donati, G. P. Missiroli, and G. Pozzi, An experiment on electron interference, American Journal of Physics 41, 639
(1973).
[7] A. Zeilinger, R. Gähler, C. G. Shull, W. Treimer, and W. Mampe, Single- and double-slit diffraction of neutrons, Rev.
Mod. Phys. 60, 1067 (1988).
[8] C. Monroe, D. M. Meekhof, B. E. King, and D. J. Wineland, A “schrödinger cat” superposition
state of an atom, Science 272, 1131 (1996), https://www.science.org/doi/pdf/10.1126/science.272.5265.1131.
[9] M. Arndt, O. Nairz, J. Vos-Andreae, C. Keller, G. van der Zouw, and A. Zeilinger, Wave–particle duality of c60 molecules,
Nature 401, 680 (1999).
[10] K. S. Lee, Y. P. Tan, L. H. Nguyen, R. P. Budoyo, K. H. Park, C. Hufnagel, Y. S. Yap, N. MÞbjerg, V. Vedral, T. Paterek,
and R. Dumke, Entanglement in a qubit-qubit-tardigrade system, New Journal of Physics 24, 123024 (2022).
[11] R. Schnabel, Einstein-podolsky-rosen–entangled motion of two massive objects, Phys. Rev. A 92, 012126 (2015).
[12] H. Salecker and E. P. Wigner, Quantum limitations of the measurement of space-time distances, Phys. Rev. 109, 571
(1958).
[13] S. Weinberg, The Quantum Theory of Fields, Vol. 1 (Cambridge University Press, 1995).