计算的原子
为量子计算机编程现在任何人都可以在自己家里做。
但是要创造什么呢?量子程序到底是什么?确切地说,什么是量子计算机?
这些问题可以通过与标准数字计算机进行比较来回答。不幸的是,大多数人实际上也不理解数字计算机是如何工作的。在本文中,我们将了解这些设备背后的基本原理。为了帮助我们稍后过渡到量子计算,我们将使用与量子计算相同的工具。
如果想使用本页中的代码,请先运行以下Python代码:
from qiskit import QuantumCircuit, assemble, Aer
from qiskit.visualization import plot_histogram
1. 将信息拆分为比特
我们首先需要了解比特的概念。它们被设计成世界上最简单的字母。只需要两个字符,0和1,就可以表示任何信息。
数就是一个例子。你可能习惯于用一个由0、1、2、3、4、5、6、7、8、9这10位数字组成的字符串来表示一个数。在这串数字中,每个数字表示这个数字包含10的某次方的次数。例如,当我们写9213时,我们的意思是
$$9000+200+10+3$$
或者,用一种强调十的幂的方式来表示
$$(9×10^3)+(2×10^2)+(1×10^1)+(3×10^0)$$
虽然我们通常基于数字10来使用这个系统,但我们也可以很容易地使用一个基于任何其他数字的系统。例如,二进制系统是以数字2为基础的。这意味着使用两个字符0和1将数字表示为2的幂的倍数。例如,9213变成10001111111101,因为
$$
\begin{split}
9213=(1×2^{13})+(0×2^{12})+(0×2^{11})+(0×2^{10})+(1×2^9)+(1×2^8)+(1×2^7)\
+(1×2^6)+(1×2^5)+(1×2^4)+(1×2^3)+(1×2^2)+(0×2^1)+(1×2^0)
\end{split}
$$
在这里,我们将数字表示为2,4,8,16,32等的倍数,而不是10,100,1000等。
from qiskit_textbook.widgets import binary_widget
binary_widget(nbits=5)
这些比特串,也就是二进制串,不仅可以用来表示数字。例如,有一种方法可以使用比特来表示任何文本。对于任何想要使用的字母、数字或标点符号,都可以使用这个表找到最多8位的对应字符串。虽然这些都是很随意的,但却是一个被广泛认可的标准。事实上,这就是通过互联网将这篇文章传输给你的方式。
这就是所有信息在计算机中的表现方式。无论是数字、字母、图像还是声音,它们都以二进制字符串的形式存在。
和我们的标准数字计算机一样,量子计算机也是基于同样的基本思想。主要的区别在于它们使用的是量子比特,量子比特是比特在量子力学中的延伸。在本教科书的其余部分,我们将探索什么是量子比特,它们可以做什么,以及它们是如何做到这一点的。然而,在本节中,我们根本不会讨论量子。所以,我们就像使用比特一样使用量子比特。
快速练习
-
想一个数字,并尝试用二进制写下来。
-
如果你有n个比特,它们可以处于多少种不同的状态?
2. 以图表示的计算
无论我们使用的是量子位还是比特,我们都需要对它们进行操作,以便将我们的输入转化为我们需要的输出。对于只有很少比特的最简单的程序,可以用电路图(circuit diagram)来表示这个过程。左边是输入,右边是输出,中间是用神秘符号表示的运算。这些操作被称为“门”,主要是由于历史原因。
下面是一个标准的、基于位的计算机的电路示例。你不需要理解它是做什么的。它应该能让你对这些电路有个大致的了解。
对于量子计算机,我们使用相同的基本思想,但对于如何表示输入、输出和用于运算的符号有不同的约定。这是表示上述相同过程的量子电路。

在本节的其余部分,我们将解释如何构建电路。最后,您将知道如何创建上述电路,它是做什么的,以及为什么它是有用的。
3. 你的第一个量子电路
在电路中,我们通常需要做三件事:首先,对输入进行编码,然后进行一些实际计算,最后提取输出。对于你的第一个量子电路,我们将专注于最后一件事。我们首先创建一个具有8个量子比特和8个输出的电路。
qc_output = QuantumCircuit(8)
这个我们称之为qc_output的电路,是由Qiskit使用QuantumCircuit创建的。QuantumCircuit以量子电路中的量子比特数作为参数。
量子电路中输出的提取是使用名为measure_all()的操作完成的。每次测量都告诉特定的量子比特给特定的输出比特一个输出。命令qc_output.measure_all()向电路qc_output中的每个量子比特添加一个测量值,并添加一些用于写入输出的经典比特。
qc_output.measure_all()
现在我们的电路中有一些东西,让我们来看看它。
qc_output.draw(initial_state=True)
量子比特总是被初始化为给出输出0。由于我们没有对上面电路中的量子比特做任何操作,这正是我们测量它们时将得到的结果。我们可以通过多次运行电路并将结果绘制成直方图来观察。我们会发现结果总是00000000:每个量子比特都是0。
sim = Aer.get_backend('aer_simulator')
result = sim.run(qc_output).result()
counts = result.get_counts()
plot_histogram(counts)

之所以运行多次并以直方图的形式展示结果,是因为量子计算机的结果可能具有一些随机性。在这种情况下,由于我们没有做任何量子操作,所以我们只能确定地得到00000000的结果。
请注意,这个结果来自量子模拟器,量子模拟器是一个计算理想量子计算机会怎么做的标准计算机。模拟只能用于少量的量子比特(~30个量子比特),但它们仍然是你在设计你的第一个量子电路时非常有用的工具。要在真正的设备上运行,你只需要将Aer.get_backend('aer_simulator')替换为你想要使用的设备的后端对象。
4. 示例:创建加法器电路
4.1 对输入进行编码
现在让我们看看如何将不同的二进制字符串编码为输入。为此,我们需要使用所谓的非门。这是你在计算机中能做的最基本的操作。它只是翻转位值:将0变成1,1变成0。对于量子比特,是一个称为x的操作来做非的工作。
下面我们创建一个专门用于编码工作的新电路,称之为qc_encode。现在,我们只指定量子比特的数量。
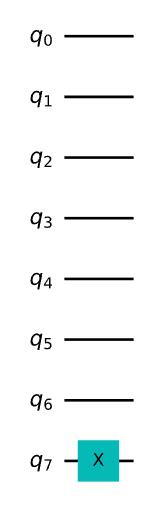
qc_encode = QuantumCircuit(8)
qc_encode.x(7)
qc_encode.draw()
提取结果可以使用我们之前的电路:qc_output。
qc_encode.measure_all()
qc_encode.draw()
现在我们可以运行组合电路并查看结果。
sim = Aer.get_backend('aer_simulator')
result = sim.run(qc_encode).result()
counts = result.get_counts()
plot_histogram(counts)

现在,我们的计算机输出的是字符串10000000。
我们翻转的是位于字符串最左边的第7位量子比特。这是因为Qiskit从右到左对字符串中的位进行编号。有些人更喜欢用相反的方式对其位进行编号,但当我们使用比特来表示数字时,Qiskit系统当然有它的优势。具体来说,这意味着第7位量子比特告诉我们数字中有多少个$2^7$。所以通过翻转这个位,我们现在在简单的8位计算机中写出了数字128。
现在试着为自己写另一个数字。例如,你可以写你的年龄。只需使用搜索引擎找出这个数字的二进制形式(如果它包含“0b”,则忽略它),然后如果你的年龄小于128,则在左侧添加一些0。
qc_encode = QuantumCircuit(8)
qc_encode.x(1)
qc_encode.x(5)
qc_encode.draw()
现在我们知道如何在计算机中编码信息。下一步是处理它:获取我们已编码的输入,并将其转化为我们需要的输出。
4.2记住如何做加法
要想把输入转化为输出,我们需要解决一个问题。让我们做一些基本的计算。在小学,你将学习如何处理大型数学问题,并把它们分解成易于处理的小问题。例如,你将如何解决以下问题?
$9213$
$+$ $1854$
$=$ $???$
一种方法是从右到左逐位计算。从3+4开始
$9213$
$+$ $1854$
$=$ $???7$
然后是1+5
$9213$
$+$ $1854$
$=$ $??67$
然后2+8=10。因为这是一个两位数的答案,所以我们需要进位。
$9213$
$+$ $1854$
$=$ $?067$
$¹$
最后是9+1+1=11,得到答案
$9213$
$+$ $1854$
$=$ $11067$
$¹$
这可能只是一个简单的加法,但它展示了所有算法背后的原理。无论算法是为了解决数学问题还是处理文本或图像,我们总是将大任务分解为小而简单的步骤。
为了在计算机上运行,算法需要被编译成尽可能最小和最简单的步骤。为了看看它们是什么样子,让我们再做一次上面的加法问题,不过这次使用二进制。
$10001111111101$
$+$ $00011100111110$
$=$ $???$
注意,第二个数字的左侧有一串额外的0。这只是为了使两个字符串具有相同的长度。
我们的第一个任务是对右边的列执行1+0。在二进制中,和在任何数字系统中一样,答案是1。对于第二列的0+1,我们得到了相同的结果。
$10001111111101$
$+$ $00011100111110$
$=$ $???11$
接下来是1+1。你肯定知道,1+1=2。在二进制中,数字2被写为10,因此需要两个比特。这意味着我们需要进位1,就像十进制中10的进位一样。
$10001111111101$
$+$ $00011100111110$
$=$ $???011$
$¹$
下一列要求我们计算1+1+1。这意味着将三个数字相加,因此对我们的计算机来说,事情变得复杂了。但我们仍然可以将其编译为更简单的操作,并且只需要将两个位相加。对于这个,我们可以从前两个1开始。
$1$
$+$ $1$
$=$ $10$
现在我们需要把这个10加到最后一个1上,这可以用我们常用的遍历列的方法来完成。
$10$
$+$ $01$
$=$ $11$
最后的结果是11(也就是3)。
现在我们可以回到问题的其余部分。随着上面的结果是11,我们有另一个进位。
$10001111111101$
$+$ $00011100111110$
$=$ $???1011$
$¹$$¹$
现在我们要做另一个1+1+1。但我们已经知道怎么做了,所以这没什么大不了的。
事实上,到目前为止,我们已经知道如何去做了。这是因为,如果你把所有东西分解为两个比特相加,那么你需要的计算就只有四种情况。下面是四个基本的和(我们将用两个比特来表示所有的答案)。
$0+0 = 00 (在十进制中,这表示0+0=0)$
$0+1 = 01 (在十进制中,这表示0+1=1)$
$1+0 = 01 (在十进制中,这表示1+0=1)$
$1+1 = 10 (在十进制中,这表示1+1=2)$
这叫做半加法器。如果我们的计算机可以实现这一点,并且可以将许多半加法器连接在一起,它将可以计算任何加法。
4.3 使用Qiskit做加法
让我们使用Qiskit制作我们自己的半加法器。这将包括一部分电路对输入进行编码,一部分电路执行算法,以及一部分电路提取结果。当我们想要使用新的输入时,第一部分将需要更改,但其余部分将始终保持不变。
我们要加的两个比特被编码在量子比特0和1中。上面的例子在这两个量子比特中都编码了1,因此它试图找到1+1的解。结果将是一个包含两个比特的字符串,我们将从量子比特2和3中读出,并分别存储在经典比特0和1中。剩下的就是填写实际的程序,它位于中间的空白区域。
图中的虚线只是用来区分电路的不同部分(尽管它们也可以有更有趣的用途)。它们是通过使用barrier指令生成的。
计算机的基本组成部分被称为逻辑门。我们已经使用了NOT门,但这还不足以实现我们的半加法器。我们只能用它来手动写出答案。由于我们希望计算机为我们做实际的计算,所以我们还需要一些更强大的门。
为了了解我们需要什么,让我们再看看半加器需要做什么。
$0+0 = 00$
$0+1 = 01$
$1+0 = 01$
$1+1 = 10$
这四个答案中最右边的位完全取决于相加的两个位是相同的还是不的。所以对于0+0和1+1,相加的两位是相同的,结果最右边的位是0。对于0+1和1+0,相加的两位不相同,最右边的位是1。
为了使我们的解决方案的这一部分正确,我们需要一个能够判断两个位是否相同的东西。传统上,在数字计算的研究中,这被称为异或(XOR)门。
| Input 1 | Input 2 | XOR Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
在量子计算机中,异或门的工作是由受控非(controlled-NOT)门完成的。因为这个名字很长,我们通常就叫它CNOT。在Qiskit中,它的名字是cx,甚至更短。在电路图中,它如下图所示。
qc_cnot = QuantumCircuit(2)
qc_cnot.cx(0,1)
qc_cnot.draw()

这适用于一对量子比特。其中一个充当控制量子比特(带有小点的那个)。另一个充当目标量子比特(带有内部有一个+的大圆圈的那个)。
有多种方法可以解释CNOT的效果。一种是看它的两个输入比特是否相同或不同。接下来,它用答案覆盖目标量子比特。如果它们相等,则目标值为0;如果它们不相等,则目标值为1。
另一种解释CNOT的方法是,如果控制量子比特为1,则在目标量子比特上执行NOT操作,否则不执行任何操作。这个解释和前面的解释一样有效(事实上,正是这个解释赋予了这个门的名字)。
通过尝试每个可能的输入来尝试CNOT。例如,这是一个用输入01测试CNOT的电路。
qc = QuantumCircuit(2,2)
qc.x(0)
qc.cx(0,1)
qc.measure(0,0)
qc.measure(1,1)
qc.draw()

如果你执行这个电路,会发现输出是11。我们可以认为这种情况的发生是因为以下原因之一。
-
CNOT计算输入值是否不同并发现它们是不同的,这意味着它想输出1。它通过重写量子比特1(记住,它在比特串的左边)的状态来实现这一点,将01变为11。
-
CNOT看到量子比特0处于状态1,因此对量子比特1应用一个NOT。这将量子比特1的0翻转为1,因此01变为11。
下面的表格显示了CNOT门所有可能的输入和相应的输出:
| Input(q1 q0) | Output(q1 q0) |
|---|---|
| 00 | 00 |
| 01 | 11 |
| 10 | 10 |
| 11 | 01 |
对于我们的半加法器,我们不想覆盖我们的一个输入。相反,我们想把结果写在另一对量子比特上。为此,我们可以使用两个CNOT。
qc_ha = QuantumCircuit(4,2)
# encode inputs in qubits 0 and 1
qc_ha.x(0) # For a=0, remove this line. For a=1, leave it.
qc_ha.x(1) # For b=0, remove this line. For b=1, leave it.
qc_ha.barrier()
# use cnots to write the XOR of the inputs on qubit 2
qc_ha.cx(0,2)
qc_ha.cx(1,2)
qc_ha.barrier()
# extract outputs
qc_ha.measure(2,0) # extract XOR value
qc_ha.measure(3,1)
qc_ha.draw()

现在我们已经完成了一个完全可以工作的半加法器的一半。我们只剩下另一个输出比特未完成:将存在于量子比特3上的那位。
如果你再看一下这四种可能的和,你会注意到只有一种情况是1而不是0:1+1=10。只有当加的两位都是1时才会发生。
为了计算这部分输出,我们可以让计算机看看两个输入是否都是1。如果它们是——而且仅当它们是——我们需要在量子位3上做一个NOT门。这将仅在这种情况下将其翻转为所需的值1,为我们提供所需的输出。
为此,我们需要一个新的门:类似于CNOT,但由两个量子比特控制而不是一个。仅当两个控制项都处于状态1时,这将对目标量子比特执行NOT。这个新的门叫做Toffoli。对于那些熟悉布尔逻辑门的人来说,它基本上是一个与(AND)门。
在Qiskit中,Toffoli用ccx指令表示。
qc_ha = QuantumCircuit(4,2)
# encode inputs in qubits 0 and 1
qc_ha.x(0) # For a=0, remove the this line. For a=1, leave it.
qc_ha.x(1) # For b=0, remove the this line. For b=1, leave it.
qc_ha.barrier()
# use cnots to write the XOR of the inputs on qubit 2
qc_ha.cx(0,2)
qc_ha.cx(1,2)
# use ccx to write the AND of the inputs on qubit 3
qc_ha.ccx(0,1,3)
qc_ha.barrier()
# extract outputs
qc_ha.measure(2,0) # extract XOR value
qc_ha.measure(3,1) # extract AND value
qc_ha.draw()

在这个例子中,我们计算的是1+1,因为两个输入位都是1。让我们看看会得到什么。
qobj = assemble(qc_ha)
counts = sim.run(qobj).result().get_counts()
plot_histogram(counts)
/home/divs/.local/lib/python3.8/site-packages/qiskit/utils/deprecation.py:62: DeprecationWarning: Using a qobj for run() is deprecated as of qiskit-aer 0.9.0 and will be removed no sooner than 3 months from that release date. Transpiled circuits should now be passed directly using `backend.run(circuits, **run_options).
return func(*args, **kwargs)

结果是10,这是数字2的二进制表示。我们已经建造了一台计算机,可以解决著名的数学问题1+1!
现在你可以尝试使用其他三种可能的输入,并证明我们的算法对它们也能给出正确的结果。
半加法器包含了加法所需的一切。使用NOT、CNOT和Toffoli门,我们可以创建任意大小的数字集的加法程序。
这三个门足以完成计算中的所有其他工作。事实上,我们甚至可以不使用CNOT。此外,只有在创建值为1的比特时才真正需要非门。Toffoli门本质上是数学的原子。它是最简单的元素,所有其他解决问题的技术都可以由它编译而来。
正如我们将看到的,在量子计算中,我们分裂了原子。
import qiskit.tools.jupyter
%qiskit_version_table
/home/divs/.local/lib/python3.8/site-packages/qiskit/aqua/init.py:86: DeprecationWarning: The package qiskit.aqua is deprecated. It was moved/refactored to qiskit-terra For more information see https://github.com/Qiskit/qiskit-aqua/blob/main/README.md#migration-guide
warn_package(‘aqua’, ‘qiskit-terra’)
版本信息
| Qiskit Software | Version |
|---|---|
| qiskit-terra | 0.18.2 |
| qiskit-aer | 0.9.0 |
| qiskit-ignis | 0.6.0 |
| qiskit-ibmq-provider | 0.16.0 |
| qiskit-aqua | 0.9.5 |
| qiskit | 0.30.0 |
| qiskit-nature | 0.2.1 |
| qiskit-finance | 0.2.1 |
| qiskit-optimization | 0.2.2 |
| qiskit-machine-learning | 0.2.1 |
| System information | |
| -----: | ----: |
| Python | 3.8.10 (default, Jun 2 2021, 10:49:15) [GCC 9.4.0] |
| OS | Linux |
| CPUs | 2 |
| Memory (Gb) | 7.521877288818359 |
| Sun Oct 03 22:50:56 2021 IST |