Qiskit汉化-3.5 Quantum Fourier Transform

LuZLouis · March 6, 2023, 1:24pm

量子傅里叶变换

在本教程中，我们将介绍量子傅里叶变换(QFT)，推导电路，并使用Qiskit实现它。我们展示了如何在模拟器和五量子比特设备上运行QFT。

1. 简介

傅里叶变换在整个经典计算中有许多不同的版本，从信号处理到数据压缩到复杂性理论。量子傅里叶变换(QFT)是波函数振幅上的离散傅里叶变换的量子实现。它是许多量子算法的一部分，最著名的是肖尔分解算法和量子相位估计。

离散傅里叶变换作用于向量 (x_0，…)， x_{N-1}) 并将其映射到向量 (y_0，…， y_{N-1}) 根据公式

y_k = \frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}x_j\omega_N^{jk}

其中 \omega_N^{jk} = e^{2\pi i \frac{jk}{N}} 。

类似地，量子傅里叶变换作用于量子态 \vert X\rangle = \sum_{j=0}^{N-1} x_j \vert j \rangle ，并根据公式将其映射到量子态 \vert Y\rangle = \sum_{k=0}^{N-1} y_k \vert k \rangle

y_k = \frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}x_j\omega_N^{jk}

\omega_N^{jk} 定义如上所示。注意，只有状态的振幅受到这种变换的影响。

这也可以表示为映射:

\vert j \rangle \mapsto \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}\omega_N^{jk} \vert k \rangle

或者是酉矩阵:

U_{QFT} = \frac{1}{\sqrt{N}} \sum_{j=0}^{N-1} \sum_{k=0}^{N-1} \omega_N^{jk} \vert k \rangle \langle j \vert

2. 直觉

量子傅里叶变换(QFT)在两个基之间变换，计算(Z)基和傅里叶基。H门是单量子比特QFT，它在Z基状态 |0\rangle 和 |1\rangle 之间转换为X基状态 |{+}\rangle 和 $|{-}\rangle$。同样地，计算基中的所有多量子比特状态在傅里叶基中都有相应的状态。QFT就是在这些基之间变换的函数。

|\text{State in Computational Basis}\rangle \quad \xrightarrow[]{\text{QFT}} \quad |\text{State in Fourier Basis}\rangle

\text{QFT}|x\rangle = |\widetilde{x}\rangle

(我们经常用波浪线(~)来表示傅里叶基中的状态)

2.1傅里叶基计数:

在计算基础上，我们使用 |0\rangle 和 |1\rangle 的状态将数字存储为二进制:

注意不同量子比特变化的频率;最左边的量子比特随着数字的每一次增加而翻转，下一个每2次增加一次，第三个每4次增加一次，依此类推。在傅里叶基中，我们使用围绕z轴的不同旋转来存储数字:

我们想要存储的数字决定了每个量子比特围绕z轴旋转的角度。在 |\widetilde{0}\rangle 状态下，所有量子位都处于 |{+}\rangle 状态。如上例所示，要在4个量子比特上编码状态 |\widetilde{5}\rangle ，我们将最左边的量子比特旋转 \tfrac{5}{2^n} = \tfrac{5}{16} 一周 ( \tfrac{5}{16}\times 2\pi 弧度)。下一个量子位被翻倍( \tfrac{10}{16}\times 2\pi 弧度，或 10/16 一周)，之后的量子位的角度被翻倍，依此类推。

同样，请注意每个量子比特变化的频率。在这种情况下，最左边的量子比特(qubit 0)频率最低，最右边的频率最高。

3. 例1:1量子比特QFT

考虑上述定义的QFT算符如何作用于单个量子比特状态 \vert\psi\rangle = \alpha \vert 0 \rangle + \beta \vert 1 \rangle 。在本例中， x_0 = \alpha ， x_1 = \beta ，和 N = 2 。然后,

y_0 = \frac{1}{\sqrt{2}}\left( \alpha \exp\left(2\pi i\frac{0\times0}{2}\right) + \beta \exp\left(2\pi i\frac{1\times0}{2}\right) \right) = \frac{1}{\sqrt{2}}\left(\alpha + \beta\right)

和

y_1 = \frac{1}{\sqrt{2}}\left( \alpha \exp\left(2\pi i\frac{0\times1}{2}\right) + \beta \exp\left(2\pi i\frac{1\times1}{2}\right) \right) = \frac{1}{\sqrt{2}}\left(\alpha - \beta\right)

这样最终的结果就是状态

U_{QFT}\vert\psi\rangle = \frac{1}{\sqrt{2}}(\alpha + \beta) \vert 0 \rangle + \frac{1}{\sqrt{2}}(\alpha - \beta) \vert 1 \rangle

这个操作正是在量子比特上应用哈达玛运算符(H)的结果:

H = \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}

如果我们将H运算符应用于状态 \vert\psi\rangle = \alpha \vert 0 \rangle + \beta \vert 1 \rangle ，我们得到新的状态:

\frac{1}{\sqrt{2}}(\alpha + \beta) \vert 0 \rangle + \frac{1}{\sqrt{2}}(\alpha - \beta) \vert 1 \rangle \equiv \tilde{\alpha}\vert 0 \rangle + \tilde{\beta}\vert 1 \rangle

注意哈达玛门如何对状态的振幅进行 N = 2 的离散傅里叶变换。

4. 量子傅里叶变换

当N更大时量子傅里叶变换是什么样的?让我们推导 N=2^ N ，$QFT_N$ 作用于状态 \vert x \rangle = \vert x_1\ldots x_n \rangle 的变换，其中 x_1 是最高位。这个数学是为那些觉得它有用的人准备的，如果你纠结于它，那么不要担心;只要你理解了第2部分中的直觉，你就可以直接进入下一部分。

\begin{aligned} QFT_N\vert x \rangle & = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1}\omega_N^{xy} \vert y \rangle \\ & = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} e^{2 \pi i xy / 2^n} \vert y \rangle ~\text{因为}\: \omega_N^{xy} = e^{2\pi i \frac{xy}{N}} \:\text{和}\: N = 2^n \\ & = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} e^{2 \pi i \left(\sum_{k=1}^n y_k/2^k\right) x} \vert y_1 \ldots y_n \rangle \:\text{ * 用分数二进制表示法重写}\: y = y_1\ldots y_n, y/2^n = \sum_{k=1}^n y_k/2^k \\ & = \frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} \prod_{k=1}^n e^{2 \pi i x y_k/2^k } \vert y_1 \ldots y_n \rangle \:\text{将和的指数展开为指数的乘积之后} \\ & = \frac{1}{\sqrt{N}} \bigotimes_{k=1}^n \left(\vert0\rangle + e^{2 \pi i x /2^k } \vert1\rangle \right) \:\text{重新排列和积，并展开} \sum_{y=0}^{N-1} = \sum_{y_1=0}^{1}\sum_{y_2=0}^{1}\ldots\sum_{y_n=0}^{1} \\ & = \frac{1}{\sqrt{N}} \left(\vert0\rangle + e^{\frac{2\pi i}{2}x} \vert1\rangle\right) \otimes \left(\vert0\rangle + e^{\frac{2\pi i}{2^2}x} \vert1\rangle\right) \otimes \ldots \otimes \left(\vert0\rangle + e^{\frac{2\pi i}{2^{n-1}}x} \vert1\rangle\right) \otimes \left(\vert0\rangle + e^{\frac{2\pi i}{2^n}x} \vert1\rangle\right) \end{aligned}

这是我们在直觉部分看到的动画的数学描述:

5. 实现QFT的电路

实现QFT的电路使用了两个门。第一个是单量子比特哈达玛门，H

从上面示例1的讨论中，您已经看到 H 对单量子比特状态 \vert x_k\rangle 的作用是

H\vert x_k \rangle = \frac{1}{\sqrt{2}}\left(\vert0\rangle + \exp\left(\frac{2\pi i}{2}x_k\right)\vert1\rangle\right)

第二个是两个量子位控制的旋转 CROT_k ，以块对角线形式给出

CROT_k = \left[\begin{matrix} I&0\\ 0&UROT_k\\ \end{matrix}\right]

其中

UROT_k = \left[\begin{matrix} 1&0\\ 0&\exp\left(\frac{2\pi i}{2^k}\right)\\ \end{matrix}\right]

CROT_k 对两个量子比特状态 \vert x_l x_j\rangle 的作用，其中第一个量子比特是控制，第二个量子比特是目标，由

CROT_k\vert 0x_j\rangle = \vert 0x_j\rangle

和

CROT_k\vert 1x_j\rangle = \exp\left( \frac{2\pi i}{2^k}x_j \right)\vert 1x_j\rangle

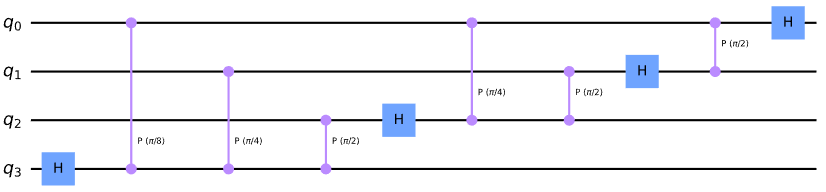
给定这两个门，实现n量子比特QFT的电路如下所示。

电路的工作原理如下。我们从n个量子比特的输入状态 \vert x_1x_2\ldots x_n\rangle 开始。

在量子比特1上的第一个哈达玛门之后，状态从输入状态转换为

H_1\vert x_1x_2\ldots x_n\rangle = \frac{1}{\sqrt{2}} \left[\vert0\rangle + \exp\left(\frac{2\pi i}{2}x_1\right)\vert1\rangle\right] \otimes \vert x_2x_3\ldots x_n\rangle

在量子位2控制的量子位1上的 UROT_2 门后，状态转换为

\frac{1}{\sqrt{2}} \left[\vert0\rangle + \exp\left(\frac{2\pi i}{2^2}x_2 + \frac{2\pi i}{2}x_1\right)\vert1\rangle\right] \otimes \vert x_2x_3\ldots x_n\rangle

在量子比特 n 控制的量子比特1上应用最后一个 UROT_n 门后，状态变为

\frac{1}{\sqrt{2}} \left[\vert0\rangle + \exp\left( \frac{2\pi i}{2^n}x_n + \frac{2\pi i}{2^{n-1}}x_{n-1} + \ldots + \frac{2\pi i}{2^2}x_2 + \frac{2\pi i}{2}x_1 \right) \vert1\rangle\right] \otimes \vert x_2x_3\ldots x_n\rangle

注意的是

x = 2^{n-1}x_1 + 2^{n-2}x_2 + \ldots + 2^1x_{n-1} + 2^0x_n

我们可以把上面的状态写成

\frac{1}{\sqrt{2}} \left[\vert0\rangle + \exp\left( \frac{2\pi i}{2^n}x \right) \vert1\rangle\right] \otimes \vert x_2x_3\ldots x_n\rangle

在对量子位 2\ldots n 应用类似的门序列后，我们发现最终状态为:

\frac{1}{\sqrt{2}} \left[\vert0\rangle + \exp\left( \frac{2\pi i}{2^n}x \right) \vert1\rangle\right] \otimes \frac{1}{\sqrt{2}} \left[\vert0\rangle + \exp\left( \frac{2\pi i}{2^{n-1}}x \right) \vert1\rangle\right] \otimes \ldots \otimes \frac{1}{\sqrt{2}} \left[\vert0\rangle + \exp\left( \frac{2\pi i}{2^{2}}x \right) \vert1\rangle\right] \otimes \frac{1}{\sqrt{2}} \left[\vert0\rangle + \exp\left( \frac{2\pi i}{2^{1}}x \right) \vert1\rangle\right]

这正是上面推导的输入状态的QFT，但注意的是，在输出状态下，量子位的顺序是相反的。

6. 例2:3量子比特QFT

为 \vert y_3y_2y_1\rangle = QFT_8\vert x_3x_2x_1\rangle 创建电路的步骤如下:

对 \vert x_1 \rangle 应用一个哈达玛门

|\psi_1\rangle = \vert x_3\rangle \otimes \vert x_2\rangle \otimes \frac{1}{\sqrt{2}} \left[ \vert0\rangle + \exp\left(\frac{2\pi i}{2}x_1\right) \vert1\rangle\right]

根据 \vert x_2\rangle ，应用 UROT_2 门到 \vert x_1\rangle

|\psi_2\rangle = \vert x_3\rangle \otimes \vert x_2\rangle \otimes \frac{1}{\sqrt{2}} \left[ \vert0\rangle + \exp\left( \frac{2\pi i}{2^2}x_2 + \frac{2\pi i}{2}x_1 \right) \vert1\rangle\right]

应用 UROT_3 门到 \vert x_1\rangle ，取决于 \vert x_3\rangle

|\psi_2\rangle = \vert x_3\rangle \otimes \vert x_2\rangle \otimes \frac{1}{\sqrt{2}} \left[ \vert0\rangle + \exp\left( \frac{2\pi i}{2^2}x_2 + \frac{2\pi i}{2}x_1 \right) \vert1\rangle\right]

对 \vert x_2 \rangle 应用一个哈达玛门

|\psi_4\rangle = \vert x_3\rangle \otimes \frac{1}{\sqrt{2}} \left[ \vert0\rangle + \exp\left( \frac{2\pi i}{2}x_2 \right) \vert1\rangle\right] \otimes \frac{1}{\sqrt{2}} \left[ \vert0\rangle + \exp\left( \frac{2\pi i}{2^3}x_3 + \frac{2\pi i}{2^2}x_2 + \frac{2\pi i}{2}x_1 \right) \vert1\rangle\right]

根据 \vert x_3\rangle ，应用 UROT_2 门到 \vert x_2\rangle

|\psi_5\rangle = \vert x_3\rangle \otimes \frac{1}{\sqrt{2}} \left[ \vert0\rangle + \exp\left( \frac{2\pi i}{2^2}x_3 + \frac{2\pi i}{2}x_2 \right) \vert1\rangle\right] \otimes \frac{1}{\sqrt{2}} \left[ \vert0\rangle + \exp\left( \frac{2\pi i}{2^3}x_3 + \frac{2\pi i}{2^2}x_2 + \frac{2\pi i}{2}x_1 \right) \vert1\rangle\right]

对 \vert x_3 \rangle 应用一个哈达玛门

|\psi_6\rangle = \frac{1}{\sqrt{2}} \left[ \vert0\rangle + \exp\left( \frac{2\pi i}{2}x_3 \right) \vert1\rangle\right] \otimes \frac{1}{\sqrt{2}} \left[ \vert0\rangle + \exp\left( \frac{2\pi i}{2^2}x_3 + \frac{2\pi i}{2}x_2 \right) \vert1\rangle\right] \otimes \frac{1}{\sqrt{2}} \left[ \vert0\rangle + \exp\left( \frac{2\pi i}{2^3}x_3 + \frac{2\pi i}{2^2}x_2 + \frac{2\pi i}{2}x_1 \right) \vert1\rangle\right]

请记住输出状态相对于所需QFT的相反顺序。因此，我们必须反转量子比特的顺序(在这种情况下，交换 y_1 和 y_3 )。

7. 关于QFT电路形式的一些注意事项

上面的例子演示了 N=2^ N 的一种非常有用的QFT形式。请注意，只有最后一个量子位依赖于所有其他输入量子位的值，后面的每一个比特对输入量子位的依赖越来越小。这在QFT的物理实现中变得很重要，在QFT中，最近邻耦合比量子位之间的远程耦合更容易实现。

此外，随着QFT电路变得越来越大，花在做越来越小的旋转上的时间也越来越多。事实证明，我们可以忽略某个阈值以下的旋转，仍然可以得到不错的结果，这被称为近似QFT。这在物理实现中也很重要，因为减少操作数量可以大大减少退相干和潜在的门错误。

8.Qiskit实现

在Qiskit中，上面讨论中使用的 CROT 门的实现是一个可控相位旋转门。这个门在OpenQASM中定义为

CP(\theta) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & e^{i\theta}\end{bmatrix}

因此，从上面讨论的 CROT_k 门到 CP 门的映射可以从公式中找到

\theta = 2\pi/2^k = \pi/2^{k-1}

8.1关于3量子比特的例子


import numpy as np

from numpy import pi

# importing Qiskit

from qiskit import QuantumCircuit, transpile, assemble, Aer, IBMQ

from qiskit.providers.ibmq import least_busy

from qiskit.tools.monitor import job_monitor

from qiskit.visualization import plot_histogram, plot_bloch_multivector

在推广到n-量子比特情况之前，为3-量子比特情况编写相关代码是有用的。首先，我们必须定义量子电路:


qc = QuantumCircuit(3)

注意: 请记住，Qiskit的最低有效位具有最低的索引(0)，因此，电路将变成第5节中的图像的水平镜像。首先，我们对量子比特2应用h门:


qc.h(2)

qc.draw()

接下来，如果量子位1处于$|1\rangle$的状态，我们想再转一个四分之一圈


qc.cp(pi/2, 1, 2) # CROT from qubit 1 to qubit 2

qc.draw()

如果最低有效量子位(0)为 |1\rangle ，则再转8圈


qc.cp(pi/4, 0, 2) # CROT from qubit 2 to qubit 0

qc.draw()

有了这个量子位，我们现在可以忽略它，重复这个过程，对量子位0和1使用相同的逻辑:


qc.h(1)

qc.cp(pi/2, 0, 1) # CROT from qubit 0 to qubit 1

qc.h(0)

qc.draw()

最后，我们必须交换量子比特0和2来完成QFT:


qc.swap(0,2)

qc.draw()

8.2通用QFT函数

现在我们将在Qiskit中为QFT创建一个通用电路。创建像这样的大型通用电路才是Qiskit的亮点。

更容易构建一个电路，用量子比特颠倒实现QFT，然后交换它们;我们将从创建正确旋转量子比特的函数开始。让我们从3个量子比特的例子开始，通过正确旋转最重要的量子比特(具有最高索引的量子比特):


def qft_rotations(circuit, n):

if n == 0: # Exit function if circuit is empty

return circuit

n -= 1 # Indexes start from 0

circuit.h(n) # Apply the H-gate to the most significant qubit

for qubit in range(n):

# For each less significant qubit, we need to do a

# smaller-angled controlled rotation:

circuit.cp(pi/2**(n-qubit), qubit, n)

让我们看看效果如何:


qc = QuantumCircuit(4)

qft_rotations(qc,4)

qc.draw()

我们可以使用下面的小部件来查看这个电路是如何随着电路中的量子比特数量而缩放的:


from qiskit_textbook.widgets import scalable_circuit

scalable_circuit(qft_rotations)

太棒了!这是QFT的第一部分。现在我们已经正确地旋转了最高位量子比特，我们需要正确地旋转第二最高位量子比特。然后我们必须处理第三个最重要的问题，以此类推。但是为什么要写更多的代码呢?当我们到达qft_rotation()函数的末尾时，我们可以使用相同的代码在下一个n-1个量子比特上重复这个过程:


def qft_rotations(circuit, n):

"""Performs qft on the first n qubits in circuit (without swaps)"""

if n == 0:

return circuit

n -= 1

circuit.h(n)

for qubit in range(n):

circuit.cp(pi/2**(n-qubit), qubit, n)

# At the end of our function, we call the same function again on

# the next qubits (we reduced n by one earlier in the function)

qft_rotations(circuit, n)

# Let's see how it looks:

qc = QuantumCircuit(4)

qft_rotations(qc,4)

qc.draw()

这很简单!函数直接或间接调用自身的过程称为递归。它可以极大地简化代码。我们可以通过下面的小部件再次看到是如何缩放的：


scalable_circuit(qft_rotations)

最后，我们需要在QFT函数的末尾添加互换，以匹配QFT的定义。我们将把它合并到最终函数qft()中:


def swap_registers(circuit, n):

for qubit in range(n//2):

circuit.swap(qubit, n-qubit-1)

return circuit

def qft(circuit, n):

"""QFT on the first n qubits in circuit"""

qft_rotations(circuit, n)

swap_registers(circuit, n)

return circuit

# Let's see how it looks:

qc = QuantumCircuit(4)

qft(qc,4)

qc.draw()

这是量子傅里叶变换的广义电路。我们可以通过下面的小部件再次看到是如何缩放的：


scalable_circuit(qft)

我们现在要演示这个电路是正确工作的。要做到这一点，我们必须首先在计算基础上编码一个数字。我们可以看到二进制中的数字5是101:


bin(5)

“0 b101”

(0b提醒我们这是一个二进制数)。让我们把它编码到我们的量子比特中:


# Create the circuit

qc = QuantumCircuit(3)

# Encode the state 5

qc.x(0)

qc.x(2)

qc.draw()

让我们使用aer模拟器检查量子比特的状态:


sim = Aer.get_backend("aer_simulator")

qc_init = qc.copy()

qc_init.save_statevector()

statevector = sim.run(qc_init).result().get_statevector()

plot_bloch_multivector(statevector)

最后，让我们使用QFT函数来查看量子比特的最终状态:


qft(qc,3)

qc.draw()


qc.save_statevector()

statevector = sim.run(qc).result().get_statevector()

plot_bloch_multivector(statevector)

可以看出QFT函数是正确工作的。比较状态

|\widetilde{0}\rangle = |{+}{+}{+}\rangle ，量子位0旋转了 \tfrac{5}{8} 一圈，量子位1旋转了 \tfrac{10}{8} 一圈(相当于 \tfrac{1}{4} 一圈)，量子位2旋转了 \tfrac{20}{8} 一圈(相当于 \tfrac{1}{2} 一圈)。

8.3在真实量子设备上运行QFT

如果我们试着在一台真实的设备上运行8.2节末尾的电路，结果将是完全随机的，因为所有的量子位都是 $|0\rangle$和$|1\rangle$ 的相等叠加。如果我们想要演示和研究QFT在真实硬件上的工作，我们可以创建状态 |\widetilde{5}\rangle ，如8.2节末尾所示，反向运行QFT，并验证输出是状态 |5\rangle 。

首先，让我们使用Qiskit来轻松地反转我们的QFT操作:


def inverse_qft(circuit, n):

"""Does the inverse QFT on the first n qubits in circuit"""

# First we create a QFT circuit of the correct size:

qft_circ = qft(QuantumCircuit(n), n)

# Then we take the inverse of this circuit

invqft_circ = qft_circ.inverse()

# And add it to the first n qubits in our existing circuit

circuit.append(invqft_circ, circuit.qubits[:n])

return circuit.decompose() # .decompose() allows us to see the individual gates

现在让我们把量子位置于 |\widetilde{5}\rangle 的状态:


nqubits = 3

number = 5

qc = QuantumCircuit(nqubits)

for qubit in range(nqubits):

qc.h(qubit)

qc.p(number*pi/4,0)

qc.p(number*pi/2,1)

qc.p(number*pi,2)

qc.draw()

我们可以看到这确实会得到傅里叶态 |\widetilde{5}\rangle :


qc_init = qc.copy()

qc_init.save_statevector()

sim = Aer.get_backend("aer_simulator")

statevector = sim.run(qc_init).result().get_statevector()

plot_bloch_multivector(statevector)

最后，让我们应用逆QFT:


qc = inverse_qft(qc, nqubits)

qc.measure_all()

qc.draw()


# Load our saved IBMQ accounts and get the least busy backend device with less than or equal to nqubits

IBMQ.load_account()

provider = IBMQ.get_provider(hub='ibm-q')

backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= nqubits

and not x.configuration().simulator

and x.status().operational==True))

print("least busy backend: ", backend)

最不繁忙的后端:ibmq_sydney


shots = 2048

transpiled_qc = transpile(qc, backend, optimization_level=3)

job = backend.run(transpiled_qc, shots=shots)

job_monitor(job)

任务状态:任务已成功运行


counts = job.result().get_counts()

plot_histogram(counts)

我们(希望)看到最高概率的结果是101

9. 问题

通过准备傅里叶状态 |\widetilde{5}\rangle 来测试上述QFT的实现，其中 \text{QFT}^{\dagger}|\widetilde{5}\rangle = |101\rangle 。尝试找到状态 |a\rangle ，使 \text{QFT}^{\dagger}|a\rangle = |100\rangle 。
查找状态 |b\rangle ，使 \text{QFT}^{\dagger}|b\rangle = |011\rangle 。
尝试编写没有递归的QFT函数。使用Qiskit的单一模拟器来验证您的结果。

10. 参考文献

M. Nielsen和I. Chuang，量子计算和量子信息，剑桥信息和自然科学系列(剑桥大学出版社，剑桥，2000)。


import qiskit.tools.jupyter

%qiskit_version_table