Qiskit-汉化3.6 Quantum Phase Estimation

Dora Dōjo
1

量子相位估计

量子相位估计是量子计算中最重要的子程序之一。它是许多量子算法的核心构建块。该算法的目标如下:

给定酉算子 U ，算法估计 U\vert\psi \rangle =e^{\boldsymbol{2\pi i} \theta}|\psi \rangle 。其中 |\psi\rangle 是一个特征向量， e^{\boldsymbol{2\pi i}\theta} 是对应的特征值。由于 U 是酉，它的所有特征值的范数都是1。

1. 概述

用于相位估计的一般量子电路如下所示。顶部寄存器包含t个“计数”量子比特，底部寄存器包含状态为 |\psi\rangle 的量子比特:

1
11964×948 56.4 KB

1.1 直觉

量子相位估计算法利用相位反冲来写入 U

(在傅里叶基中)到计数寄存器中的 t 个量子位。然后我们使用逆QFT将其从傅里叶基转化为我们可以测量的计算基。

我们记得(从QFT章节中)，在傅里叶基中，最上面的量子比特在 0 和 2^t 之间计数时完成了一个完整的旋转。为了计算出一个介于 0 和 2^t 之间的数字 x ，我们将这个量子比特绕z轴旋转 \tfrac{x}{2^t} 。对于下一个量子比特，我们旋转 \tfrac{2x}{2^t} ，然后对第三个量子比特旋转 \tfrac{4x}{2^t} 。

2
22224×1668 193 KB

当我们使用一个量子比特来控制 U 门时，量子比特将(由于反冲)成比例地转向相位 e^{2i\pi\theta} 。我们可以使用连续的 CU -门来重复这个旋转适当的次数，直到我们在傅里叶基中将相位θ编码为 0 和 2^t 之间的数字。

然后我们简单地使用 QFT^\dagger 将其转换为计算基。

1.2数学基础

如上所述，该电路估计酉算子 U 的相位。它在 U\vert\psi \rangle =e^{\boldsymbol{2\pi i}\theta} |\psi\rangle 中估计 \theta ，其中 |\psi\rangle 是一个特征向量， e^{\boldsymbol{2\pi i}\theta} 是对应的特征值。该电路的工作步骤如下:

!. 设置: \vert\psi\rangle 在一组量子比特寄存器中。计数寄存器中另一组 n 量子比特，我们将在其上存储 2^n\theta :

|\psi_0\rangle = \lvert 0 \rangle^{\otimes n} \lvert \psi \rangle

!!. 叠加:在计数寄存器上应用 n 位的哈达玛门操作 H^{\otimes n} :

|\psi_1\rangle = {\frac {1}{2^{\frac {n}{2}}}}\left(|0\rangle +|1\rangle \right)^{\otimes n} \lvert \psi \rangle

!!!. 受控酉操作:我们需要引入受控酉操作 CU ，它只在目标寄存器对应的控制位为 |1\rangle 时对其应用酉操作符 U 。由于 U 是一个具有特征向量 |\psi\rangle 的酉算子，使得 U|\psi \rangle =e^{\boldsymbol{2\pi i} \theta}|\psi \rangle ，这意味着:

U^{2^{j}}|\psi \rangle =U^{2^{j}-1}U|\psi \rangle =U^{2^{j}-1}e^{2\pi i\theta }|\psi \rangle =\cdots =e^{2\pi i2^{j}\theta }|\psi \rangle

应用所有 n 控制操作 $CU^{2^j}$与$0\leq j\leq n-1$ ，并使用关系 |0\rangle \otimes |\psi \rangle +|1\rangle \otimes e^{2\pi i\theta}|\psi \rangle =\left(|0\rangle +e^{2\pi i\theta}|1\rangle \right)\otimes |\psi \rangle :

\begin{aligned} |\psi_{2}\rangle & =\frac {1}{2^{\frac {n}{2}}} \left(|0\rangle+{e^{\boldsymbol{2\pi i} \theta 2^{n-1}}}|1\rangle \right) \otimes \cdots \otimes \left(|0\rangle+{e^{\boldsymbol{2\pi i} \theta 2^{1}}}\vert1\rangle \right) \otimes \left(|0\rangle+{e^{\boldsymbol{2\pi i} \theta 2^{0}}}\vert1\rangle \right) \otimes |\psi\rangle\\\\ & = \frac{1}{2^{\frac {n}{2}}}\sum _{k=0}^{2^{n}-1}e^{\boldsymbol{2\pi i} \theta k}|k\rangle \otimes \vert\psi\rangle \end{aligned}

其中 k 表示n位二进制数的整数表示。

iv. 傅里叶逆变换:请注意，上面的表达式正是应用量子傅里叶变换的结果，就像我们在量子傅里叶变换及其Qiskit实现的笔记本上推导的那样。回想一下，QFT将n个量子比特的输入状态 \vert x\rangle 映射到输出为

QFT\vert x \rangle = \frac{1}{2^\frac{n}{2}} \left(\vert0\rangle + e^{\frac{2\pi i}{2}x} \vert1\rangle\right) \otimes \left(\vert0\rangle + e^{\frac{2\pi i}{2^2}x} \vert1\rangle\right) \otimes \ldots \otimes \left(\vert0\rangle + e^{\frac{2\pi i}{2^{n-1}}x} \vert1\rangle\right) \otimes \left(\vert0\rangle + e^{\frac{2\pi i}{2^n}x} \vert1\rangle\right)

将上面表达式中的 x 替换为 2^n\theta ，得到的表达式恰好是上面第2步中导出的表达式。因此，为了恢复状态 \vert2^n\theta\rangle ，在辅助寄存器上应用傅里叶逆变换。我们发现，这样做

\vert\psi_3\rangle = \frac {1}{2^{\frac {n}{2}}}\sum _{k=0}^{2^{n}-1}e^{\boldsymbol{2\pi i} \theta k}|k\rangle \otimes | \psi \rangle \xrightarrow{\mathcal{QFT}_n^{-1}} \frac {1}{2^n}\sum _{x=0}^{2^{n}-1}\sum _{k=0}^{2^{n}-1} e^{-\frac{2\pi i k}{2^n}(x - 2^n \theta)} |x\rangle \otimes |\psi\rangle

v. 测量:上面的表达式在 x = 2^n\theta 附近达到峰值。对于 2^n\theta 为整数的情况，在计算基中测量会以高概率给出辅助寄存器中的相位:

|\psi_4\rangle = | 2^n \theta \rangle \otimes | \psi \rangle

对于 2^n\theta 不是整数的情况，可以表明上述表达式仍然在 x = 2^n\theta 附近达到峰值，概率优于 $4/\pi^2 $ 约40%。

2. 示例:t型门

让我们以一个我们非常熟悉的门， T -门，并使用量子相位估计来估计它的相位。你会记得 T -门在状态 |1\rangle 中添加了一个相位 e^\frac{i\pi}{4} :

T|1\rangle = \begin{bmatrix} 1 & 0\\ 0 & e^\frac{i\pi}{4}\\ \end{bmatrix} \begin{bmatrix} 0\\ 1\\ \end{bmatrix} = e^\frac{i\pi}{4}|1\rangle

因为QPE会给我们 θ ，其中:

T|1\rangle = e^{2i\pi\theta}|1\rangle

我们希望找到:

\theta = \frac{1}{8}

在这个例子中，我们将使用三个量子比特并获得准确的结果(不是估计!)

2.1创建电路

让我们首先准备我们的环境:


#initialization

import matplotlib.pyplot as plt

import numpy as np

import math

# importing Qiskit

from qiskit import IBMQ, Aer, transpile, assemble

from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister

# import basic plot tools

from qiskit.visualization import plot_histogram

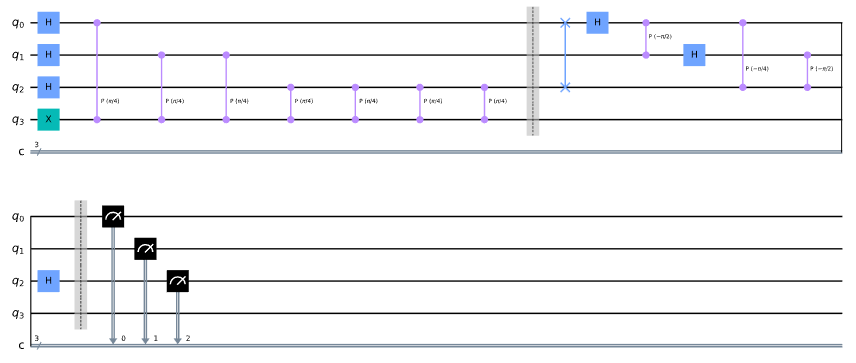
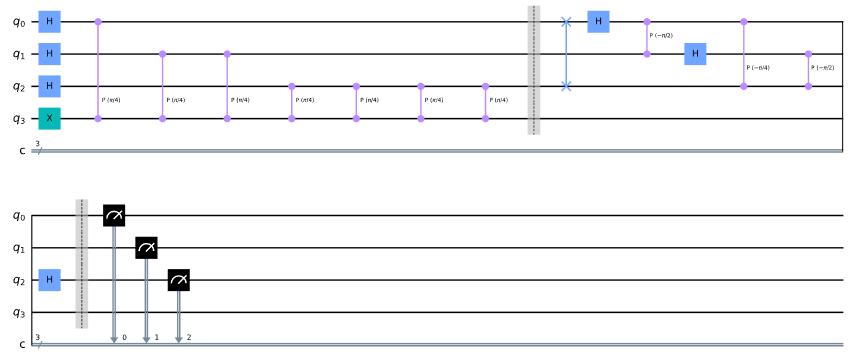
现在，建立量子电路。我们将使用四个量子位——量子位 0 到 2 作为计算量子比特，量子比特3作为酉算子( T )的本征态。

我们通过应用 X 门初始化 \vert\psi\rangle = \vert1\rangle :


qpe = QuantumCircuit(4, 3)

qpe.x(3)

qpe.draw()

3

接下来，我们将哈达玛门应用于计数量子比特:


for qubit in range(3):

qpe.h(qubit)

qpe.draw()

4

接下来我们进行受控的酉运算。记住:Qiskit的量子比特排序与上图相反。


repetitions = 1

for counting_qubit in range(3):

for i in range(repetitions):

qpe.cp(math.pi/4, counting_qubit, 3); # This is CU

repetitions *= 2

qpe.draw()

5
5837×246 3.77 KB

我们应用量子傅里叶逆变换来转换计数寄存器的状态。这里我们提供了 QFT^\dagger 的代码:


def qft_dagger(qc, n):

"""n-qubit QFTdagger the first n qubits in circ"""

# Don't forget the Swaps!

for qubit in range(n//2):

qc.swap(qubit, n-qubit-1)

for j in range(n):

for m in range(j):

qc.cp(-math.pi/float(2**(j-m)), m, j)

qc.h(j)

然后我们测量计数寄存器:


qpe.barrier()

# Apply inverse QFT

qft_dagger(qpe, 3)

# Measure

qpe.barrier()

for n in range(3):

qpe.measure(n,n)



qpe.draw()

6
6856×363 10.7 KB

2.2结果


aer_sim = Aer.get_backend('aer_simulator')

shots = 2048

t_qpe = transpile(qpe, aer_sim)

qobj = assemble(t_qpe, shots=shots)

results = aer_sim.run(qobj).result()

answer = results.get_counts()

plot_histogram(answer)

7

我们可以确定地得到一个结果(001)，它转换为十进制数:1。我们现在需要用结果(1)除以 2^n 得到 \theta :

\theta = \frac{1}{2^3} = \frac{1}{8}

这正是我们所期望的结果!

3.示例:提高精度

3.1问题

我们使用 \theta = \frac{1}{3} 来代替 T -门。我们像上一个例子一样设置电路:


# Create and set up circuit

qpe2 = QuantumCircuit(4, 3)

# Apply H-Gates to counting qubits:

for qubit in range(3):

qpe2.h(qubit)

# Prepare our eigenstate |psi>:

qpe2.x(3)

# Do the controlled-U operations:

angle = 2*math.pi/3

repetitions = 1

for counting_qubit in range(3):

for i in range(repetitions):

qpe2.cp(angle, counting_qubit, 3);

repetitions *= 2

# Do the inverse QFT:

qft_dagger(qpe2, 3)

# Measure of course!

for n in range(3):

qpe2.measure(n,n)

qpe2.draw()

8
8867×368 5.28 KB 


# Let's see the results!

aer_sim = Aer.get_backend('aer_simulator')

shots = 4096

t_qpe2 = transpile(qpe2, aer_sim)

qobj = assemble(t_qpe2, shots=shots)

results = aer_sim.run(qobj).result()

answer = results.get_counts()

plot_histogram(answer)

9

我们期待结果 \theta = 0.3333\dots ，我们看到最有可能的结果是010(bin) = 2(dec)和011(bin) = 3(dec)。这两个结果将分别告诉我们 \theta = 0.25 (误差25%)和 \theta = 0.375 (误差13%)。 θ 的真实值位于我们可以从计数位得到的值之间，这给我们带来了不确定性和不精确性。

3.2解决方案

为了获得更高的精度，我们只需添加更多的计数量子比特。我们将再添加两个计数量子比特:


# Create and set up circuit

qpe3 = QuantumCircuit(6, 5)

# Apply H-Gates to counting qubits:

for qubit in range(5):

qpe3.h(qubit)

# Prepare our eigenstate |psi>:

qpe3.x(5)

# Do the controlled-U operations:

angle = 2*math.pi/3

repetitions = 1

for counting_qubit in range(5):

for i in range(repetitions):

qpe3.cp(angle, counting_qubit, 5);

repetitions *= 2

# Do the inverse QFT:

qft_dagger(qpe3, 5)

# Measure of course!

qpe3.barrier()

for n in range(5):

qpe3.measure(n,n)

qpe3.draw()

10
10844×1023 27.9 KB 


# Let's see the results!

aer_sim = Aer.get_backend('aer_simulator')

shots = 4096

t_qpe3 = transpile(qpe3, aer_sim)

qobj = assemble(t_qpe3, shots=shots)

results = aer_sim.run(qobj).result()

answer = results.get_counts()

plot_histogram(answer)

11

现在最可能的两个测量值是01011(十进制11)和01010(十进制10)。测量这些结果会告诉我们 θ 是:

\theta = \frac{11}{2^5} = 0.344,\;\text{ or }\;\; \theta = \frac{10}{2^5} = 0.313

这两个结果与 \frac{1}{3} 的差异分别为3%和6%。更高的精度!

4. 用真实设备进行实验

4.1 电路2.1

我们可以在真实的设备上运行2.1节中的电路，让我们回忆一下这个电路:


qpe.draw()

12
12858×357 10.6 KB 


IBMQ.load_account()

from qiskit.tools.monitor import job_monitor

provider = IBMQ.get_provider(hub='ibm-q')

santiago = provider.get_backend('ibmq_santiago')

# Run with 2048 shots

shots = 2048

t_qpe = transpile(qpe, santiago, optimization_level=3)

job = santiago.run(t_qpe, shots=shots)

job_monitor(job)

任务状态:任务已成功运行


# get the results from the computation

results = job.result()

answer = results.get_counts(qpe)

plot_histogram(answer)

13

我们希望看到最可能的结果是001，这是我们期望从模拟器得到的结果。与模拟器不同的是，有可能测量到001以外的东西，这是由于量子计算机中的噪声和门误差。

5. 练习

  1. 用不同的门尝试以上的实验( CNOT ，受控- S ，受控- T^\dagger )，你期望的结果是什么?你得到了什么结果?

  2. 尝试受控- Y -门的实验，你得到了你想要的结果吗?(提示:请确保 |\psi\rangle 是 Y 的特征态!)

6. 期待

量子相位估计算法似乎毫无意义，因为我们必须知道 θ 才能在我们的量子计算机上执行受控- U 操作。我们将在后面的章节中看到，有可能创建我们不知道 θ 的电路，而学习θ可以告诉我们一些非常有用的东西(最著名的是如何分解一个数!)

7. 参考文献

[1] Michael A. Nielsen and Isaac L. Chuang. 2011. Quantum Computation and Quantum Information: 10th Anniversary Edition (10th ed.). Cambridge University Press, New York, NY, USA.

8. 贡献者

03/20/2020 - HwajungKang (@HwajungKang) -修复了量子比特排序的不一致


import qiskit.tools.jupyter

%qiskit_version_table

版本信息

Qiskit Software Version
Qiskit 0.27.0
Terra 0.17.4
Aer 0.8.2
Ignis 0.6.0
Aqua 0.9.2
IBM Q Provider 0.14.0
System information
Python 3.7.7 (default, May 6 2020, 04:59:01) [Clang 4.0.1 (tags/RELEASE_401/final)]
OS Darwin
CPUs 8
Memory (Gb) 32.0

Wed Jun 16 09:47:53 2021 BST