Qiskit-汉化3.8 Grover's Algorithm

Dora Dōjo
1

Grover 算法

在本节中，我们将介绍 Grover 算法，以及如何使用它来解决非结构化搜索问题。然后使用 Qiskit 实现了量子算法，并在模拟器和设备上运行。

1.简介

你可能听说过，量子计算机相对于经典计算机的众多优势之一是其搜索数据库的速度更快。Grover 算法展示了这种能力。这个算法可以将一个非结构化搜索问题的平方加速，但它的用途不止于此；它可以作为一种通用技巧或子程序，为其他各种算法获得平方运行时间的改进。这被称为振幅放大技巧。

非结构化搜索

假设你有一个很大的列表，包含 N 个元素。在这些元素中，我们希望定位一个具有独特属性的元素;我们称这个为获胜者 W 。把列表中的每一项想象成一个特定颜色的盒子。假设列表中的所有物品都是灰色的，除了赢家 W (紫色)。

1
14000×1068 153 KB

要找到紫色的盒子——标记的项目——使用经典计算，人们必须检查这些盒子的平均 N/2 ，在最坏的情况下，所有它们的 N 。然而，在量子计算机上，我们可以使用 Grover 的振幅放大技巧在大约 \sqrt{N} 步骤中找到标记的项。在长列表中查找标记项时，平方加速确实大大节省了时间。此外，该算法不使用 list 的内部结构，这使得它是泛型的；这就是为什么它立即为许多经典问题提供了平方量子加速。

创建 Oracle

对于这本教科书中的示例，我们的“数据库”由我们的量子比特可能处于的所有可能的计算基础状态组成。例如，如果我们有 3 个量子比特，我们的列表是状态 |000\rangle， |001\rangle， \dots |111\rangle(即 |0\rangle \rightarrow |7\rangle)。

Grover 算法解决了向解决方案状态添加负相位的 oracle。例如，对于任何状态 |x\rangle 的计算基础:

U_\omega|x\rangle = \bigg\{ \begin{aligned} \phantom{-}|x\rangle \quad \text{if} \; x \neq \omega \\ -|x\rangle \quad \text{if} \; x = \omega \\ \end{aligned}

该 oracle 将是一个对角矩阵，其中与标记项对应的项将具有负相位。例如，如果我们有三个量子比特和
\omega = \text{101} ，我们的 oracle 将得到矩阵:

U_\omega = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{aligned} \\ \\ \\ \\ \\ \\ \leftarrow \omega = \text{101}\\ \\ \\ \\ \end{aligned}

Grover 的算法之所以如此强大，是因为它可以很容易地将问题转换为这种形式的预言。有许多计算问题很难找到解，但验证解相对容易。例如，我们可以通过检查满足所有规则来轻松验证数独的解决方案。对于这些问题，我们可以创建一个函数 f ，它接受一个建议的解决方案 x ，并返回 f(x) = 0 ，如果 x 不是一个解决方案(x \neq \omega)，则返回 f(x) = 1 。我们的 oracle 可以被描述为:

U_\omega|x\rangle = (-1)^{f(x)}|x\rangle

oracle 的矩阵是一个对角线矩阵，形式如下:

U_\omega = \begin{bmatrix} (-1)^{f(0)} & 0 & \cdots & 0 \\ 0 & (-1)^{f(1)} & \cdots & 0 \\ \vdots & 0 & \ddots & \vdots \\ 0 & 0 & \cdots & (-1)^{f(2^n-1)} \\ \end{bmatrix}
建造Grover Oracle(点击扩展)

如果有经典的函数 f(x) ，可以将其转换为如下形式的可逆电路:

1
如果我们在状态 |{-}\rangle 中初始化output量子比特，阶段回退效应将其转换为 Grover oracle(类似 Deutsch-Jozsa oracle 的工作方式):

2

然后我们忽略辅助(|{-}\rangle)量子比特。

在下一章中，我们的目标是教授该算法的核心概念。我们将创建一个预先知道 \omega 的 oracle 示例，而不用担心这些 oracle 是否有用。在本章末尾，我们将介绍一个创建 oracle 来解决问题(数独)的简短示例。

振幅放大

那么算法是如何工作的呢?在查看物品列表之前，我们不知道被标记的物品在哪里。因此，任何对其位置的猜测都是一样准确的，可以用一个均匀的叠加来表示: |s \rangle = \frac{1}{\sqrt{N}} \sum_{x = 0}^{N -1} | x \rangle.

如果此时我们在标准基 \{| x \rangle \} 中测量，根据第五量子定律，这个叠加态将坍缩到 \frac{1}{N} = \frac{1}{2^ N} 的任意一个基态。因此，我们猜对 w 的概率是 2^n 中的 1 ，这是可以预期的。因此，平均来说，我们需要尝试大约 N/2 = 2^{N -1} 次才能猜出正确的物品。

进入一个叫做振幅放大的过程，这就是量子计算机如何显著提高这个概率的方法。这个过程延长(放大)被标记项目的振幅，从而缩小其他项目的振幅，以便测量最终状态将近乎确定地返回正确的项目。

该算法具有很好的几何解释，可以通过两次反射在二维平面上产生旋转。我们需要考虑的两个特殊状态是获胜者 | w \rangle 和均匀叠加态 | s \rangle 。这两个向量在向量空间 \mathbb{C}^n 中张成一个二维平面。它们并不完全垂直，因为 | w \rangle 也出现在振幅 N^{-1/2} 的叠加中。然而，我们可以引入一个额外的状态 |s'\rangle ，它位于这两个向量的空间中，它垂直于 | w \rangle ，它是通过删除 | w \rangle 并缩放来从 |s \rangle 得到的。

第一步：振幅放大过程从均匀叠加 | s \rangle 开始，它很容易从 | s \rangle = H^{\otimes n} | 0 \rangle^n 构造出来。

1
14100×1644 190 KB

左边的图形对应于由垂直向量 |w\rangle 和 |s'\rangle 张成的二维平面，允许将初始状态表示为 |s\rangle = \sin \theta |w\rangle + \cos \theta |s'\rangle ,其中 \theta = \arcsin \langle s |w\rangle = \arcsin \frac{1}{\sqrt{N}} 。右边的图形是状态 | s \rangle 的振幅的条形图。

第二步：我们将 oracle 反射 U_f 应用于状态 |s\rangle 。

2
24100×2000 238 KB

从几何上看，这表示状态 |s\rangle 以 s'\rangle 为轴做的对称翻转。
这种转换意味着 |w\rangle 状态前面的振幅变为负值，这反过来意味着平均振幅(由虚线表示)已经降低。

第三步：我们现在对状态 U_s = 2|s\rangle\langle s| - I 施加一个额外的反射( U_s )。此转换将状态映射到 U_s U_f| s \rangle 并完成转换。

3
34100×2000 233 KB

两个反射总是对应一个旋转。转换 U_s U_f 将初始状态 |s\rangle 旋转到获胜者 |w\rangle 。两个反射总是对应一个旋转。变换 U_s U_f 使初始状态 |s\rangle 更接近获胜者 |w\rangle 。

振幅条形图中反射 U_s 的作用可以理解为对平均振幅的反射。由于第一次反射降低了平均振幅，因此这种变换将 |w\rangle 的负振幅提高到其原始值的大约三倍，同时降低其他振幅。然后我们转到第 2 步来重复应用程序。这个过程将重复几次，以锁定获胜者。

在 t 步骤后，我们将处于 |\psi_t\rangle 状态，其中 |\psi_t\rangle = (U_s U_f)^t | s \rangle 。

我们需要旋转多少次?事实证明，大约 \sqrt{N} 旋转就足够了。当查看状态 | \psi \rangle 的振幅时，这一点就变得很清楚了。

我们可以看到 | w \rangle 的振幅随着应用程序的数量 \sim t N^{-1/2} 线性增长。

然而，由于我们处理的是振幅而不是概率，所以向量空间的维数是一个平方根。因此，在这个过程中被放大的是振幅，而不仅仅是概率。

在有多个解 M 的情况下，可以证明大约 \sqrt{(N/M)} 旋转就足够了。

4
44000×1314 235 KB

2. 示例:2 个量子比特

让我们先来看看 Grover 算法 N=4 的情况，它是用 2 个量子比特实现的。在这种特殊情况下，只需要旋转一次，就可以将初始状态 |s\rangle 旋转到获胜者 |w\rangle [3]:

  1. 根据上面的介绍，在 N=4 的情况下，我们有
\theta = \arcsin \frac{1}{2} = \frac{\pi}{6}.

  1. 经过 t 步骤，我们有

    (U_s U_\omega)^t | s \rangle = \sin \theta_t | \omega \rangle + \cos \theta_t | s' \rangle ,

    其中

    \theta_t = (2t+1)\theta.

  2. 为了得到 | \omega \rangle ，我们需要 \theta_t =\frac{\pi}{2} ，将 \theta=\frac{\pi}{6} 插入到 t=1 的结果中。这意味着在 t=1 旋转后找到了搜索的元素。

现在我们将使用一个特定的 oracle 示例。

Oracle 为 \lvert \omega \rangle = \lvert 11 \rangle

让我们看看 \lvert \omega \rangle = \lvert 11 \rangle 的情况。在本例中，oracle U_\omega 的作用如下:

U_\omega | s \rangle = U_\omega \frac{1}{2}\left( |00\rangle + |01\rangle + |10\rangle + |11\rangle \right) = \frac{1}{2}\left( |00\rangle + |01\rangle + |10\rangle - |11\rangle \right).

或者：

U_\omega = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \\ \end{bmatrix}

你可能会认出这是受控 Z 门。因此，在这个例子中，我们的 oracle 只是一个受控的 Z 门:

5

反射 U_s

为了完成电路，我们需要实现额外的反射 U_s = 2|s\rangle\langle s| - I 。因为这是对 |s\rangle 的反射，所以我们想给每个与 |s\rangle 正交的状态添加一个负相位。

我们可以这样做的一种方法是使用转换状态 |s\rangle \rightarrow |0\rangle 的操作，我们已经知道这是应用于每个量子比特的哈达玛门:

H^{\otimes n}|s\rangle = |0\rangle

然后我们应用一个电路，在与 |0\rangle 正交的状态上添加一个负相位:

U_0 \frac{1}{2}\left( \lvert 00 \rangle + \lvert 01 \rangle + \lvert 10 \rangle + \lvert 11 \rangle \right) = \frac{1}{2}\left( \lvert 00 \rangle - \lvert 01 \rangle - \lvert 10 \rangle - \lvert 11 \rangle \right)

也就是说，除了 \lvert 00 \rangle 之外，每个状态的符号都翻转了。可以很容易地验证，实现 U_0 的一种方法是以下电路:

6

最后，我们执行转换状态 |0\rangle \rightarrow |s\rangle(又是 H-门)的操作:

H^{\otimes n}U_0 H^{\otimes n} = U_s

U_s 的完整电路如下所示:

7

完整电路为\lvert w \rangle = |11\rangle

因为在 N=4 的特殊情况下只需要旋转一次，我们就可以将上述组件组合起来，为 Grover 算法构建完整的电路。

8

2.1 Qiskit 实现

我们现在为上述情况实现了 Grover 的算法，即 \lvert w \rangle = |11\rangle 的 2 个量子比特。

#initialization
import matplotlib.pyplot as plt
import numpy as np

# importing Qiskit
from qiskit import IBMQ, Aer, assemble, transpile
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit.providers.ibmq import least_busy

# import basic plot tools
from qiskit.visualization import plot_histogram

我们首先准备一个有两个量子比特的量子电路:

n = 2
grover_circuit = QuantumCircuit(n)

然后我们只需要写出上面描述的电路的命令。首先，我们需要初始化状态 |s\rangle 。让我们创建一个通用函数(用于任意数量的量子比特)，以便我们稍后可以再次使用它:

def initialize_s(qc, qubits):
    """Apply a H-gate to 'qubits' in qc"""
    for q in qubits:
        qc.h(q)
    return qc

grover_circuit = initialize_s(grover_circuit, [0,1])
grover_circuit.draw()

9

为 |w\rangle = |11\rangle 应用 Oracle。此 oracle 特定于 2 个量子比特:

grover_circuit.cz(0,1) # Oracle
grover_circuit.draw()

10

我们现在想要应用扩散器( U_s )。与初始化 |s\rangle 的电路一样，我们将创建一个通用的扩散器(用于任何数量的量子比特)，以便我们可以在稍后的其他问题中使用它。

# Diffusion operator (U_s)
grover_circuit.h([0,1])
grover_circuit.z([0,1])
grover_circuit.cz(0,1)
grover_circuit.h([0,1])
grover_circuit.draw()

11

这是我们完成的电路。

2.1.1 使用模拟器进行实验

让我们在模拟中运行电路。首先，我们可以验证我们有正确的状态向量:

sim = Aer.get_backend('aer_simulator')
# we need to make a copy of the circuit with the 'save_statevector'
# instruction to run on the Aer simulator
grover_circuit_sim = grover_circuit.copy()
grover_circuit_sim.save_statevector()
qobj = assemble(grover_circuit_sim)
result = sim.run(qobj).result()
statevec = result.get_statevector()
from qiskit_textbook.tools import vector2latex
vector2latex(statevec, pretext="|\\psi\\rangle =")
|\psi\rangle =\begin{bmatrix} 0 \\ 0 \\ 0 \\ 1\end{bmatrix}

正如预期的那样，非 |11\rangle 的每个状态的振幅都是 0，这意味着我们有 100%的机会测量
|11\rangle :

grover_circuit.measure_all()

aer_sim = Aer.get_backend('aer_simulator')
qobj = assemble(grover_circuit)
result = aer_sim.run(qobj).result()
counts = result.get_counts()
plot_histogram(counts)

12

2.1.2 用真实设备进行实验

我们可以在真实的设备上运行电路，如下所示。

# Load IBM Q account and get the least busy backend device
provider = IBMQ.load_account()
provider = IBMQ.get_provider("ibm-q")
device = least_busy(provider.backends(filters=lambda x: int(x.configuration().n_qubits) >= 3 and
                                   not x.configuration().simulator and x.status().operational==True))
print("Running on current least busy device: ", device)

在当前最不忙的设备上运行:ibmq_mumbai

# Run our circuit on the least busy backend. Monitor the execution of the job in the queue
from qiskit.tools.monitor import job_monitor
transpiled_grover_circuit = transpile(grover_circuit, device, optimization_level=3)
job = device.run(transpiled_grover_circuit)
job_monitor(job, interval=2)

任务状态:任务已成功运行

# Get the results from the computation
results = job.result()
answer = results.get_counts(grover_circuit)
plot_histogram(answer)

13

我们证实，在大多数情况下，状态 |11\rangle 是测量的。其他结果是由于量子计算中的误差。

3.示例:3 个量子比特

我们现在来看一个 Grover 算法的例子，它有 3 个量子比特，有两个标记状态 \lvert101\rangle 和 \lvert110\rangle ，具体实现参见[2]。用相位 oracle 解决这个问题的量子电路如下:

14
14866×324 12.9 KB

1.将哈达玛门应用到初始化为 \lvert000\rangle 的 3 个量子比特，以创建一个统一的叠加:

\lvert \psi_1 \rangle = \frac{1}{\sqrt{8}} \left( \lvert000\rangle + \lvert001\rangle + \lvert010\rangle + \lvert011\rangle + \lvert100\rangle + \lvert101\rangle + \lvert110\rangle + \lvert111\rangle \right)

2.使用相位 oracle 标记 \lvert101\rangle 和 \lvert110\rangle:

\lvert \psi_2 \rangle = \frac{1}{\sqrt{8}} \left( \lvert000\rangle + \lvert001\rangle + \lvert010\rangle + \lvert011\rangle + \lvert100\rangle - \lvert101\rangle - \lvert110\rangle + \lvert111\rangle \right)

3.在平均振幅周围进行反射:

  1. 将哈达玛门应用于量子比特
\lvert \psi_{3a} \rangle = \frac{1}{2} \left( \lvert000\rangle +\lvert011\rangle +\lvert100\rangle -\lvert111\rangle \right)
  1. 对量子比特应用 X 门
\lvert \psi_{3b} \rangle = \frac{1}{2} \left( -\lvert000\rangle +\lvert011\rangle +\lvert100\rangle +\lvert111\rangle \right)
  1. 在 1,2(控制)和 3(目标)量子比特之间应用一个双控制 Z 门
\lvert \psi_{3c} \rangle = \frac{1}{2} \left( -\lvert000\rangle +\lvert011\rangle +\lvert100\rangle -\lvert111\rangle \right)
  1. 对量子比特应用 X 门
\lvert \psi_{3d} \rangle = \frac{1}{2} \left( -\lvert000\rangle +\lvert011\rangle +\lvert100\rangle -\lvert111\rangle \right)
  1. 对量子比特应用哈达玛门
\lvert \psi_{3e} \rangle = \frac{1}{\sqrt{2}} \left( -\lvert101\rangle -\lvert110\rangle \right)

4.测量 3 个量子比特以检索状态 \lvert101\rangle 和 \lvert110\rangle

注意，因为有 2 个解决方案和 8 种可能性，我们只需要运行一次迭代(第 2 步和第 3 步)。

3.1 Qiskit 实现

我们现在为上面 3 量子比特的例子实现 Grover 算法，并搜索两个标记状态 \lvert101\rangle 和 \lvert110\rangle 。注意:记住，Qiskit 的量子比特顺序与此资源相反，因此绘制的电路将出现水平翻转。

我们创建一个阶段 oracle，将结果标记为 \lvert101\rangle 和 \lvert110\rangle (第 1 步)。

qc = QuantumCircuit(3)
qc.cz(0, 2)
qc.cz(1, 2)
oracle_ex3 = qc.to_gate()
oracle_ex3.name = "U$_\omega$"

在上一节中，我们使用了一个特定于 2 个量子比特的扩散器，在下面的单元中，我们将为任意数量的量子比特创建一个通用的扩散器。

详细信息：创建通用扩散器（单击以展开）

记住，我们可以从$U_0$中创建$U_s$:

U_s = H^{\otimes n} U_0 H^{\otimes n}

和一个多控Z门(MCZ)反转状态的相位$|11\dots 1\rangle$:

MCZ = \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & -1 \\ \end{bmatrix} \begin{aligned} \\ \\ \\ \leftarrow \text{将负相添加到} \; |11\dots 1\rangle\\ \end{aligned}

对每个量子比特应用x门执行转换:

\begin{aligned} |00\dots 0\rangle & \rightarrow |11\dots 1\rangle\\ |11\dots 1\rangle & \rightarrow |00\dots 0\rangle \end{aligned}

所以:

U_0 = - X^{\otimes n} (MCZ) X^{\otimes n}

使用这些属性，我们可以使用H门，X门和一个多控Z门创建 U_s :

U_s = - H^{\otimes n} U_0 H^{\otimes n} = H^{\otimes n} X^{\otimes n} (MCZ) X^{\otimes n} H^{\otimes n}

注意，我们可以忽略-1的全局相位。

def diffuser(nqubits):
    qc = QuantumCircuit(nqubits)
    # Apply transformation |s> -> |00..0> (H-gates)
    for qubit in range(nqubits):
        qc.h(qubit)
    # Apply transformation |00..0> -> |11..1> (X-gates)
    for qubit in range(nqubits):
        qc.x(qubit)
    # Do multi-controlled-Z gate
    qc.h(nqubits-1)
    qc.mct(list(range(nqubits-1)), nqubits-1)  # multi-controlled-toffoli
    qc.h(nqubits-1)
    # Apply transformation |11..1> -> |00..0>
    for qubit in range(nqubits):
        qc.x(qubit)
    # Apply transformation |00..0> -> |s>
    for qubit in range(nqubits):
        qc.h(qubit)
    # We will return the diffuser as a gate
    U_s = qc.to_gate()
    U_s.name = "U$_s$"
    return U_s

我们现在将这些部分放在一起，在电路开始时创建均匀叠加并在结束时进行测量。请注意，由于有 2 种解决方案和 8 种可能性，我们只需要运行一次迭代。

n = 3
grover_circuit = QuantumCircuit(n)
grover_circuit = initialize_s(grover_circuit, [0,1,2])
grover_circuit.append(oracle_ex3, [0,1,2])
grover_circuit.append(diffuser(n), [0,1,2])
grover_circuit.measure_all()
grover_circuit.draw()

15

3.1.1 使用模拟器进行实验

我们可以在模拟器上运行上面的电路。

sim = Aer.get_backend('aer_simulator')
# we need to make a copy of the circuit with the 'save_statevector'
# instruction to run on the Aer simulator
grover_circuit_sim = grover_circuit.copy()
grover_circuit_sim.save_statevector()
qobj = assemble(grover_circuit_sim)
result = sim.run(qobj).result()
statevec = result.get_statevector()
from qiskit_textbook.tools import vector2latex
vector2latex(statevec, pretext="|\\psi\\rangle =")

16

如我们所见，该算法发现了我们标记的状态 |101 ⟩和 | 110 ⟩。

3.1.2 用真实设备进行实验

我们可以在真实设备上运行电路，如下所示。

backend = least_busy(provider.backends(filters=lambda x: int(x.configuration().n_qubits) >= 3 and
                                   not x.configuration().simulator and x.status().operational==True))
print("least busy backend: ", backend)

最不忙的后端：ibmq_mumbai

# 在最不繁忙的后端运行我们的电路。监控队列中作业的执行
from  qiskit.tools.monitor  import  job_monitor
transpiled_grover_circuit  =  transpile ( grover_circuit ,  device ,  optimization_level = 3 )
job  =  device 。运行( transpiled_grover_circuit )
job_monitor ( job ,  interval = 2 )

任务状态:任务已成功运行

# Get the results from the computation
results = job.result()
answer = results.get_counts(grover_circuit)
plot_histogram(answer)

17

正如我们可以(希望)看到的，有更高的机会测量|101⟩和|110⟩。其他结果是由于量子计算中的误差。

4. 问题

下面的函数 grover_problem_oracle 采用多个量子比特数(n)和一个 variant ，并返回一个 n 个量子比特的 oracle。对于相同的 n 和 variant ，函数总是返回相同的 oracle。当调用 grover_problem_oracle 时，你可以通过设置 print_solutions = True 来查看每个 oracle 的解决方案。

from qiskit_textbook.problems import grover_problem_oracle
## Example Usage
n = 4
oracle = grover_problem_oracle(n, variant=1)  # 0th variant of oracle, with n qubits
qc = QuantumCircuit(n)
qc.append(oracle, [0,1,2,3])
qc.draw()

18

  1. Grover_problem_oracle (4, variant=2)使用 4 个量子比特，有 1 个解决方案。
    a.我们需要多少次迭代才能有 > 90% 的机会测量此解决方案？
    b.使用 Grover 算法找到此解决方案状态。
    C.如果我们对上面问题 1a 中计算的次数进行更多迭代，会发生什么情况？为什么？

  2. 有 2 个解决方案和 4 个量子比特，我们需要多少次迭代才能有>90%的机会测量一个解决方案?使用 oracle grover_problem_oracle(4, variant=1)(它有两个解决方案)测试您的答案。

  3. 创建一个函数 grover_solver(oracle, iterations)，将其作为输入:

    • Grover oracle 作为门 ( oracle)
    • 迭代次数为整数(iterations)并返回一个量子电路，在oracle门上执行 Grover 算法，迭代次数为iterations

5. 使用 Grover 算法求解数独

用 Grover 算法求解数独到目前为止，本章中用到的 oracle 都是在已知它们的解决方案的基础上创建的。现在我们将使用 Grover 算法来解决一个简单的问题，对此我们不一定事先知道解决方案。我们的问题是一个 2×2 二进制数独，在我们的例子中有两个简单的规则:

  • 任何列都不能两次包含相同的值
  • 任何行都不能两次包含相同的值

如果我们将数独中的每个方格分配给如下变量:

19

我们希望我们的电路输出这个数独的解决方案。

请注意，虽然使用 Grover 算法解决此问题的方法并不实用(你可能在自己的头脑中就能找到解决方案!)，但这个示例的目的是演示如何将经典的决策问题转换为 Grover 算法的 oracle。

5.1 把问题变成电路

我们想创建一个 oracle 来帮助我们解决这个问题，我们将从创建一个识别正确解决方案的电路开始。类似于我们在计算的原子中使用量子电路创建经典加法器的方式，我们只需要在量子电路上创建一个经典函数，以检查变量位的状态是否为有效解。

因为我们需要检查两列和两行，所以我们需要检查 4 个条件:

v0 ≠ v1 # 沿着上面一行检查
v2 ≠ v3 # 沿着下面一行检查
v0 ≠ v2 # 沿着左面一行检查
v1 ≠ v3 # 沿着右面一行检查

请记住，我们正在比较经典（计算基础）状态。为了方便起见，我们可以将这组比较编译成一个子句列表：

clause_list = [[0,1],
               [0,2],
               [1,3],
               [2,3]]

我们将把每个变量的值赋给电路中的一个位。为了在计算中检查这些子句，我们将使用异或门(我们在原子计算中遇到过这个)。

def XOR(qc, a, b, output):
    qc.cx(a, output)
    qc.cx(b, output)

说服自己，只有当 input0≠input1 时，下面电路中的 output0 位才会翻转:

# We will use separate registers to name the bits
in_qubits = QuantumRegister(2, name='input')
out_qubit = QuantumRegister(1, name='output')
qc = QuantumCircuit(in_qubits, out_qubit)
XOR(qc, in_qubits[0], in_qubits[1], out_qubit)
qc.draw()

20

该电路检查 input0 是否== input1，并将输出存储到 output0。为了检查每个子句，我们对 clause_list 中的每个配对重复这个电路，并将输出存储到一个新位:

# Create separate registers to name bits
var_qubits = QuantumRegister(4, name='v')  # variable bits
clause_qubits = QuantumRegister(4, name='c')  # bits to store clause-checks

# Create quantum circuit
qc = QuantumCircuit(var_qubits, clause_qubits)

# Use XOR gate to check each clause
i = 0
for clause in clause_list:
    XOR(qc, clause[0], clause[1], clause_qubits[i])
    i += 1

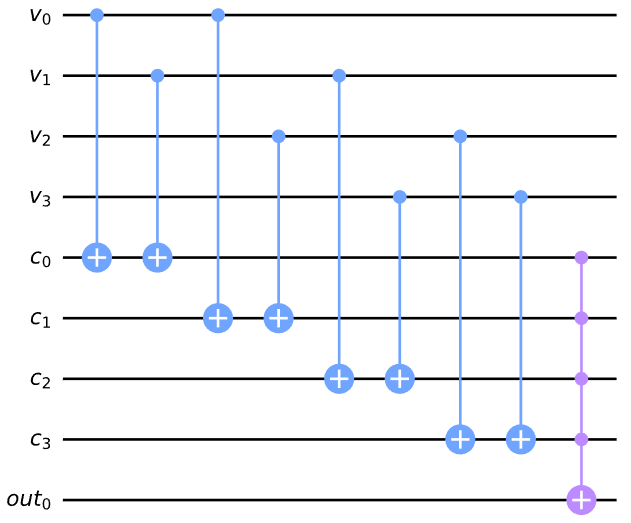
qc.draw()

21

只有在 v0, v1, v2, v3 的赋值是数独的解的情况下，位 c0, c1, c2, c3 的最终状态才都是 1。为了完成我们的检查电路，我们希望当(且仅当)所有子句都满足时，有一个位为 1，这样我们就可以只看一个位来判断我们的赋值是否是一个解。我们可以使用多重控制的托夫利门来做到这一点:

# Create separate registers to name bits
var_qubits = QuantumRegister(4, name='v')
clause_qubits = QuantumRegister(4, name='c')
output_qubit = QuantumRegister(1, name='out')
qc = QuantumCircuit(var_qubits, clause_qubits, output_qubit)

# Compute clauses
i = 0
for clause in clause_list:
    XOR(qc, clause[0], clause[1], clause_qubits[i])
    i += 1

# Flip 'output' bit if all clauses are satisfied
qc.mct(clause_qubits, output_qubit)

qc.draw()

22
22631×523 6.01 KB

上述电路以位 v0、v1、v2 和 v3 的初始赋值作为输入，所有其他位都应初始化为 0。在运行电路之后，out0 位的状态告诉我们这个赋值是否是一个解;Out0 = 0 表示分配不是一个解，Out0 = 1 表示分配是一个解。
重要提示:在继续之前，重要的是要充分理解这个电路，并确信它像上面段落中所述的那样工作。

5.2 取消计算并完成 Oracle

我们现在可以使用相位反冲将这个检查电路变成 Grover oracle 。回顾一下，我们有 3 个寄存器：

  • 一个存储我们的数独变量的寄存器（我们会说 x = v_3, v_2, v_1, v_0 )
  • 一个存储我们的子句的寄存器（从状态开始 |0000\rangle 我们将缩写为 |0\rangle )
  • 还有一个量子比特（ |\text{out}_0\rangle ) 我们用它来存储校验电路的输出。

要创建一个 oracle，我们需要我们的电路（ U_\omega ) 执行转换：

U_\omega|x\rangle|0\rangle|\text{out}_0\rangle = |x\rangle|0\rangle|\text{out}_0\oplus f(x)\rangle

如果我们将 out0 量子比特设置为叠加态 |{-}\rangle 有:

\begin{aligned} U_\omega|x\rangle|0\rangle|{-}\rangle &= U_\omega|x\rangle|0\rangle\otimes\tfrac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\\ &= |x\rangle|0\rangle\otimes\tfrac{1}{\sqrt{2}}(|0\oplus f(x)\rangle - |1\oplus f(x)\rangle) \end{aligned}

如果 f(x) = 0 ，那么我们有状态:

\begin{aligned} &= |x\rangle|0\rangle\otimes \tfrac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\\ &= |x\rangle|0\rangle|-\rangle\\ \end{aligned}

(即没有变化)。但如果 f(x) = 1 (即 x = \omega )，我们将一个负相位引入 |{-}\rangle 量子比特:

\begin{aligned} &= \phantom{-}|x\rangle|0\rangle\otimes\tfrac{1}{\sqrt{2}}(|1\rangle - |0\rangle)\\ &= \phantom{-}|x\rangle|0\rangle\otimes -\tfrac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\\ &= -|x\rangle|0\rangle|-\rangle\\ \end{aligned}

这是一个正常运行的 oracle，它使用两个状态为 |0\rangle|{-}\rangle 的辅助寄存器:

U_\omega|x\rangle|0\rangle|{-}\rangle = \Bigg\{ \begin{aligned} \phantom{-}|x\rangle|0\rangle|-\rangle \quad \text{for} \; x \neq \omega \\ -|x\rangle|0\rangle|-\rangle \quad \text{for} \; x = \omega \\ \end{aligned}

为了使我们的检查电路适应 Grover oracle，我们需要保证第二个寄存器(c)中的比特在计算后总是返回到状态 |0000\rangle 。要做到这一点，我们只需重复电路中计算子句的部分，以保证在电路运行后 c0 = c1 = c2 = c3 = 0。我们称这一步为“未计算”。

var_qubits = QuantumRegister(4, name='v')
clause_qubits = QuantumRegister(4, name='c')
output_qubit = QuantumRegister(1, name='out')
cbits = ClassicalRegister(4, name='cbits')
qc = QuantumCircuit(var_qubits, clause_qubits, output_qubit, cbits)

def sudoku_oracle(qc, clause_list, clause_qubits):
    # Compute clauses
    i = 0
    for clause in clause_list:
        XOR(qc, clause[0], clause[1], clause_qubits[i])
        i += 1

    # Flip 'output' bit if all clauses are satisfied
    qc.mct(clause_qubits, output_qubit)

    # Uncompute clauses to reset clause-checking bits to 0
    i = 0
    for clause in clause_list:
        XOR(qc, clause[0], clause[1], clause_qubits[i])
        i += 1

sudoku_oracle(qc, clause_list, clause_qubits)
qc.draw()

23
23843×448 7.47 KB

综上所述，上述电路实现了:

U_\omega|x\rangle|0\rangle|\text{out}_0\rangle = \Bigg\{ \begin{aligned} |x\rangle|0\rangle|\text{out}_0\rangle \quad \text{for} \; x \neq \omega \\ |x\rangle|0\rangle\otimes X|\text{out}_0\rangle \quad \text{for} \; x = \omega \\ \end{aligned}

如果 $|\text{out}_0\rangle = |{-}\rangle$，:

U_\omega|x\rangle|0\rangle|{-}\rangle = \Bigg\{ \begin{aligned} \phantom{-}|x\rangle|0\rangle|-\rangle \quad \text{for} \; x \neq \omega \\ -|x\rangle|0\rangle|-\rangle \quad \text{for} \; x = \omega \\ \end{aligned}

5.3 完整算法

现在剩下要做的就是将这个 oracle 放入 Grover 的算法中!

var_qubits = QuantumRegister(4, name='v')
clause_qubits = QuantumRegister(4, name='c')
output_qubit = QuantumRegister(1, name='out')
cbits = ClassicalRegister(4, name='cbits')
qc = QuantumCircuit(var_qubits, clause_qubits, output_qubit, cbits)

# Initialize 'out0' in state |->
qc.initialize([1, -1]/np.sqrt(2), output_qubit)

# Initialize qubits in state |s>
qc.h(var_qubits)
qc.barrier()  # for visual separation

## First Iteration
# Apply our oracle
sudoku_oracle(qc, clause_list, clause_qubits)
qc.barrier()  # for visual separation
# Apply our diffuser
qc.append(diffuser(4), [0,1,2,3])

## Second Iteration
sudoku_oracle(qc, clause_list, clause_qubits)
qc.barrier()  # for visual separation
# Apply our diffuser
qc.append(diffuser(4), [0,1,2,3])

# Measure the variable qubits
qc.measure(var_qubits, cbits)

qc.draw(fold=-1)

24
24863×195 13.5 KB 

# Simulate and plot results
aer_simulator = Aer.get_backend('aer_simulator')
transpiled_qc = transpile(qc, aer_simulator)
qobj = assemble(transpiled_qc)
result = aer_sim.run(qobj).result()
plot_histogram(result.get_counts())

25

有两个比特串的测量概率比其他任何一个都要高，0110和1001。这些对应于下面的赋值:

v0 = 0
v1 = 1
v2 = 1
v3 = 0

和

v0 = 1
v1 = 0
v2 = 0
v3 = 1

这是我们数独的两个解决方案!本节的目的是展示我们如何从实际问题中创建 Grover oracles。虽然这个特定的问题是微不足道的，但这个过程可以应用于任何决策问题(允许足够大的电路)。概括一下，这些步骤是:

  1. 创建一个可以识别正确解决方案的可逆经典电路

  2. 使用相位反冲和未计算将此电路变成一个 oracle

  3. 使用Grover的算法来解决这个oracle

6. 参考文献

  1. L. K. Grover (1996), “A fast quantum mechanical algorithm for database search”, Proceedings of the 28th Annual ACM Symposium on the Theory of Computing (STOC 1996), doi:10.1145/237814.237866, arXiv:quant-ph/9605043

  2. C. Figgatt, D. Maslov, K. A. Landsman, N. M. Linke, S. Debnath & C. Monroe (2017), “Complete 3-Qubit Grover search on a programmable quantum computer”, Nature Communications, Vol 8, Art 1918, doi:10.1038/s41467-017-01904-7, arXiv:1703.10535

  3. I. Chuang & M. Nielsen, “Quantum Computation and Quantum Information”, Cambridge: Cambridge University Press, 2000.

import qiskit.tools.jupyter
%qiskit_version_table

版本信息

Qiskit Software Version
Qiskit 0.27.0
Terra 0.17.4
Aer 0.8.2
Ignis 0.6.0
Aqua 0.9.2
IBM Q Provider 0.14.0
System information
Python 3.7.7 (default, May 6 2020, 04:59:01) [Clang 4.0.1 (tags/RELEASE_401/final)]
OS Darwin
CPUs 8
Memory (Gb) 32.0
Wed Jun 16 13:45:01 2021 BST